Исследование кинематической схемы механизма привода дверей. График и расчет промежуточного положения

4 Исследование кинематической схемы механизма привода дверей

В процессе работы привода дверей нас интересуют силы, действующие на механизма. Для предотвращения травмирования пассажиров и порчи личного имущества усилие закрытия и открытия дверей следует нормировать. Эта сила не должна превышать значение 200-250 Н. Для ее контроля в редукторе установлен фрикцион, от силы прижатия которого и зависит конечное усилие на створках двери при работе привода. Для определения значения и характера распределения сил, действующих на механизм, построим график зависимости конечной силы на двери от положения створки.  

Для  построения графика конечной силы F₂, действующей на края наружной створки, произведем расчет сил дверного механизма в нескольких произвольных положениях коромысла в момент закрытия дверей. Будем считать, что электродвигатель приводя в движение входной вал редуктора, создает на его выходном валу момент M, численно равный произведению силы F₁ на плечо OA. Это момент и приводит в движение весь механизм. Для определения сил действующих на дверной механизм применим принцип мгновенных центров скоростей.

Зададимся линейными приращениями точек A, B, C, D, E и угловыми приращениями точек A и B. Определив мгновенный центр P для линейных приращений dS_A и dS_B можно записать пропорцию

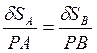,                                                           (4.1)

где РА – расстояние от точки мгновенного центра скоростей Р до точки А;

РВ – расстояние от точки мгновенного центра скоростей Р до точки В.

Тогда можно записать

dS_A cos a = dS_B cos b,                                        (4.2)

где cos a – угол между тягой AB и вектором линейного приращения dS_A;

cos b – угол между тягой AB и линейного приращения dS_B.

Определим линейное приращение dS_A точки A

dS_A = OA×d_A,                                                    (4.3)

где – d_A – угловое приращение точки A,

ОА – длинна плеча коромысла.

Определим линейное приращение dS_В точки B

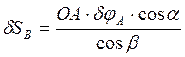.                                             (4.4)

Так как рычаг BC соединен с осью дверной створки неподвижно, то угол BCD не изменяется. Считаем, что для линейных приращений dS_B и dS_D угловое приращение будет одинаковым  и равным d_B.

Определим линейное приращение dS_D точки D

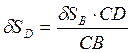.                                                     (4.5)

Для линейных приращений dS_D и dS_E можно записать уравнение

dS_D cos g = dS_E cos q,                                           (4.6)

где cos g – угол между AB и линейным приращением dS_A;

cos q– угол между AB и линейным приращением dS_B.

Определим линейное приращение dS_E

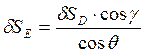.                                                   (4.7)

Полученные выражения подставим в формулу для определения линейного приращения dS_Е

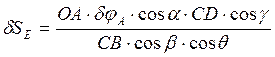.                              (4.8)

Для проведения вычислений сил действующих на механизм в различных промежуточных положениях и простоты реализации таких вычислений следует связать начальное усилие редуктора с конечной силой схождения створок. Такими величинами являются вращающий момент на выходном валу редуктора и сила F₂ с которой дверь при закрытии будет воздействовать на препятствие во время закрытия.

Момент действующий на коромысло со стороны редуктора M, Н×м и силу F₂,Н можно связать уравнением

M×d_A = F₂×dS_E.                                                  (4.9)

Тогда силу F₂, Н, можно определить по формуле

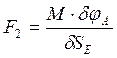.                                                        (4.10)

Запишем формулу для определения силы F₂, подставив в уравнение 4.10 полученные ранее выражения

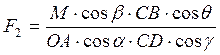 .                                      (4.11)

Для вычисления силы F_2, в некоторых промежуточных положениях механизма, определим значения перечисленных углов и занесем их в таблицу 4.1

Таблица 4.1 – Вычисление силы F₂ в процессе закрытия двери

По значениям полученной силы F₂ и расстоянию L построим график.

График и расчет промежуточного положения представлены на графическом листе 6.