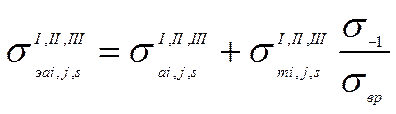Машиностроение \ Вагоны и вагонное хозяйство

Расчет сопротивления усталости рамы четырехосной платформы модели 23-469, переоборудованной под перевозку контейнеров согласно проекту 469-07.00.00.000, страница 2

2.5 Величина показателя степени m принимается согласно  «Нормам…» равным 4.

2.6 Величины амплитуд динамических напряжений, полученные в результата расчета, приводятся к эквивалентному симметричному циклу по следующей формуле

 ,                  (5)

где

-уровень амплитуд напряжений от действия вертикальных динамических сил в интервале i;

-уровень амплитуд напряжений от действия продольной ударной силы в интервале i;

-уровень амплитуд напряжений от действия погрузо - разгрузочных сил в интервале i;

-среднее значение напряжений от действия вертикальных динамических сил в интервале i;

- среднее значение напряжений от действия продольной ударной силы в интервале i;

- среднее значение напряжений от действия погрузо - разгрузочных сил в интервале i;

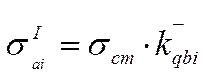2.7 Уровни амплитуд напряжений от действия вертикальных динамических сил определялись по формуле

 ,                  (6)

где

σст

-статическое напряжение от силы тяжести брутто платформы;

-средний коэффициент вертикальной динамики в интервале i.

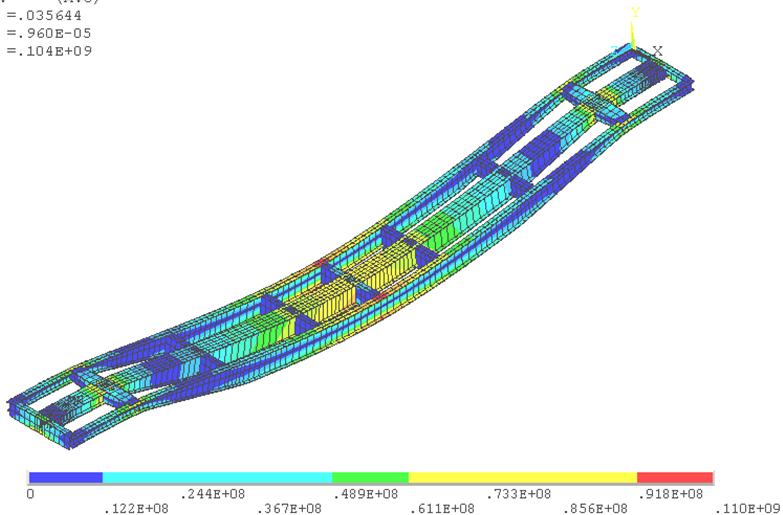
2.8 Для шкворневых и опорных узлов коэффициент вертикальной динамики определялся с учетом коэффициента γ=0,2.

2.9 Статическое напряжение от силы тяжести брутто платформы были получены из расчета методом конечных элементов рамы (к конечно-элементной модели прикладывалась только силы тяжести рамы и контейнеров 1ААА с грузом). Для расчета использовалась, конечно-элементная модель из расчета прочности                             469-07.00.00.000 РР1. Напряженно деформированное состояние рамы от действия силы тяжести брутто платформы представлено на рисунке 1.

Рис. 1 - Напряженно деформированное состояния рамы от действия силы тяжести брутто платформы

2.10 Величины статических напряжений от силы тяжести брутто платформы для исследуемых зон приведены в таблице 3.

Таблица 3 - Величины статических напряжений от силы тяжести брутто платформы

Зона

Боковая балка в зоне центральной балки

Лобовой лист в зоне хребтовой балки

Хребтовая балка в зоне шкворневой балки

σст, МПа

93

40

43

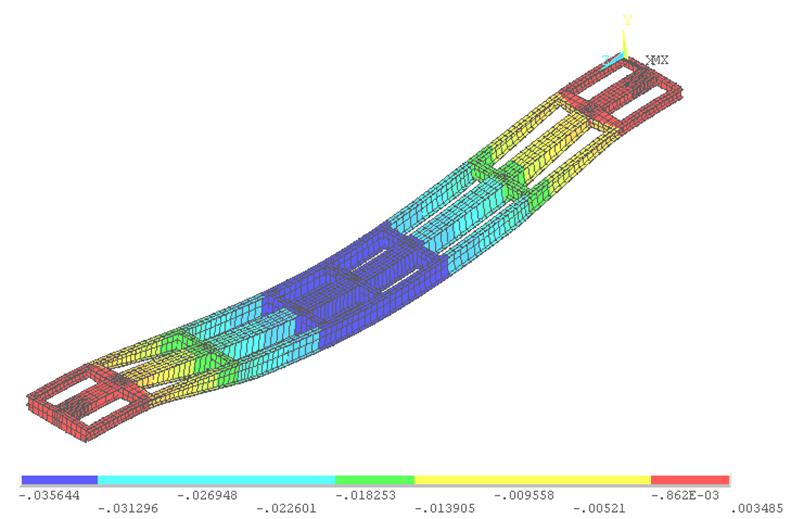
2.11 Прогибы рамы от действия силы тяжести брутто платформы представлено на рисунке 2. Максимальный прогиб составляет 0,035 м.

Рис.2 – Прогиб платформы от действия силы тяжести брутто платформы

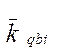2.12 Значение определялись по формулам «Норм…»

при V i < 15м/с

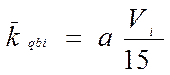,                                  (7)

при V i ≥ 15м/с

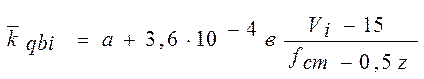,              (8)

где

а

-коэффициент, равный для элементов кузова 0,05;

в

-коэффициент, учитывающий влияние числа осей n в тележке под одним концом экипажа, определяется по формуле

                                                                       (9)

Vi

-конструкционная скорость движения, м/c;

-статический прогиб рессорного подвешивания, м.

z

-прогиб рамы (учитывается согласно «Нормам…» в случае перевозки тяжелых (более 50% грузоподъемности) сосредоточенных на длине менее половины базы вагона грузов), м.

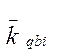2.13 В качестве Vi приняты средние скорости интервалов распределения скоростей согласно «Нормам…». Величины Vi , и  приведены в таблице 4.

Таблица 4 - Величины Vi , 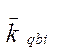и

Интервал

 скоростей

Средняя скорость Vi , м/с

Частость

0÷12,5

6,25

0,021

0,03

12,5÷15,0

13,75

0,046

0,07

15,0÷17,5

16,25

0,068

0,09

17,5÷20,0

18,75

0,104

0,12

20,0÷22,5

21,25

0,140

0,16

22,5÷25,0

23,75

0,176

0,19

25,0÷27,5

26,25

0,212

0,16

27,5÷30,0

28,75

0,248

0,10

30,0÷32,5

31,25

0,284

0,06

32,5÷35,0

33,75

0,320

0,02

Σ=1

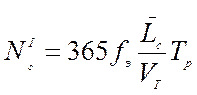2.14 Суммарное число циклов вертикальных динамических сил за срок службы определяется по формуле «Норм…»

,            (10)

где

-  центральная (эффективная) частота процесса изменения динамических напряжений, Гц, определяется по формуле

;           (11)

а

-  коэффициент для кузова, а=1,4;

g

-  ускорение свободного падения, g = 9,81 м/с2;

fст

-  статический прогиб рессорного подвешивания груженой платформы, м;

Тр

-  срок службы платформы, Тр=32 года;

-  среднесуточный пробег платформы принимался согласно статистическим данным ОАО «РЖД»,  =125 км/сутки;

VТ

-  средняя техническая скорость движения платформы,        VТ =22,4 м/с.

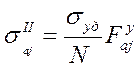2.15 При ударном взаимодействии платформы с соседними вагонами возникают быстро затухающие колебательные процессы. Уровни амплитуд напряжений от действия продольной ударной силы можно определить путем пересчета напряжений по формуле

,                                           (12)

где

-  амплитуда  напряжений, посчитанная методом конечных элементов, при ударном взаимодействии платформы с соседними вагонами, МПа;

N

-  продольная ударная сила, действующая на платформу, соответствующая полученным расчетным , МПа;

-  уровень амплитуды ударного продольного усилия на автосцепку в интервале j, МПа.
Скачать файл