Проведение непрерывного приема контроля. Выборочный приемочный контроль последовательных партий

1. про рейки

=4                                         =0.4

среднее - уровень настройки равен 4,см, стандартное отклонение - точность настройки 0,4 см доля реек нестандартной толщины:   р==0,056=5,6%

6. про деталь № 25

переписываем табл из дано, внизу продлеваем ее

разм: 21, 29,26, 23,22, 22,24, 24,24, 24,23,23,30,25, 25,30

сред:7, 18, 10,10,10,7,9,11,6,5,4,12,9,15,14

это считаем по формулам ,  R =x(max)-x(min)

По данным задачи: Для карты среднего НКГ()=20, ВКГ()=25,2, ЦЛ()=(25.2+20)/2=22.6 Для карты размахов НКГ(R)=0,  ВКГ(R)=12,  ЦЛ(R)=(0+12)/2=6

Карта среднего: ось хчисла от 1-15, у- знач среднего (или размаха)

По виду контрольных карт видно, что точки 2, 3, 12, 15 на карте среднего выходят за КГ. Значит в этих точках необходимо корректировать процесс, искать причины такого поведения процесса. По карте размахов точки №2, 14, 15 выходят за верхнюю контрольную гранияяцу, что является неприемлемым. Необходимо найти причины такого поведения процесса и проводить корректировку.

11. Проводится выборочный приемочный контроль последовательных партий. объем партии=75, AQL=1,5%, определить номера кода.

1. код Е

2. код В

2. пластмассовые шарики, настройка станка

Н₀: Н₁: Дано: а=10г, s=0,8г, a=0,5

9,88 =-0,67

Ф(z_кр)==0,475, Z_кр=1,96 – находим по таблице аспределения функции Лапласа, ½Z_н½<z_кр – Н₀ принимается, средний вес шариков в выборке незначимо отличается от заданного среднего, станок настроен правильно.

7. На машиностроительном заводе

За пределы поля допуска выходит 13+11=24 детали, это количество бракованных изделий

12. Для проведения непрерывного прием контроля найти: трехстадийный план NQL=12%, NQL=50%

3. про розетки

N=10000, g=0.944, D=0.05, s=0.4 n-?

, где u- находя из таблицы распределения функции Лапласа: Ф(u)=0,944,

u=1.91, n»228

8. При изготовлении красок

Коэффициент корреляции, где

r= 0,8979956  - коэф. корреляции

Поскольку коэф. корреляции r=0,89, близок к 1, значит между кол-вом состава и скоростью высыхания существует сильная связь, поскольку r>0, то с увеличением кол-ва состава увеличивается скорость высыхания и наоборот.

13. Проводится непрерывный приемочный контроль. Сравнить длины стадий:

NQL=2%,d=2;  3;  4.

1.Т3, NQL=2%, k=3, R=1,

2. Т5, k=2, R=2, d=4

продолжение табл в длину

4. про осветляющие химикаты 

Н₀:Н₁:

а=90%, a=0,5,

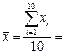81, =15.9

=-1,79

T_кр(a/2=0.025,n-1=9)=2.69 – по таблице распределения Стьюдента, ½T_н½<Tкр – Н₀ принимается, фирма была права.

9 . Проводится выборочный приемочный контроль.

Сравните объемы выборок. AQL=15.

Код выборки J

14. Для определения средней длины детали следует провести выборочное обследование методом случайного повторного отбора.

D=3, s=6, g=0,997

n-?

, где t находим по табл. распр. функции Лапласа Ф(t)=0,997,  t=2,98

n=35.5»36

5. про бракованные изделия

n=80  m=5,   g=0.954     D=5,    N=80×10=800,   D-?

Доля бракованных изделий=0,0625    s==0,242, , где t – находим из табл распр функции Лапласа Ф(t)=0,954  t=2

D=0,05, что не больше 5%.

10. Изготовитель проводит приемочный контроль 50779.71-99. партии объемом 150 единиц. Запишите принимается она или нет.

Код D

15. Выборка из большой партии электроламп содержит 100 ламп. Найти с надежностью 0,95 доверительный интервал

N=100,   =1000,  g=0.95,    s=40

D-?

, где t- находим по табл. распр. функции Лапласа: Ф(t)=0.95, t=1,96

D=7,84

Доверительный интервал

1000-7,84££1000+7,84