ВАРИАНТЫ ЗАДАЧ ДЛЯ ЛАБОРАТОРНОЙ РАБОТЫ 3
N 1
Дана система из n-линейных уравнений
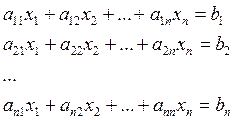 .
.
Разработать программу решения этой системы следующими методами: последовательного исключения неизвестных, простых итераций и методом Зейделя. Предполагается, что метод решения выбирается пользователем.
Метод последовательного исключения неизвестных. Процедура решает неоднородную систему n линейных алгебраических уравнений с n неизвестными:
a11 x1+a12 x2+ . . .+a1n xn=a1n+1
a21 x1+a22 x2+ . . .+a2n xn=a2n+1
. . . .
an1 x1+an2 x2+ . . .+ann xn=ann+1
Вначале находим отличный от нуля коэффициент при x1. Соответствующее уравнение переставляем с первым (если это необходимо). Получаем систему с a11 отличным от нуля. Разделив коэффициенты этого уравнения на a11, получим:
x1+b12 x2+ . . .+b1n xn=b1n+1
При помощи этого уравнения исключаем x1 из исходной системы:
a(1)22 x2+a(1)23 x3+ . . .+a(1)2n xn=a(1)2n+1
. . . .
a(1)n2 x2+a(1)n3 x3+ . . .+a(1)nn xn=a(1)nn+1
где
a(1)i j=ai j-ai 1b1 j, i,j= 2...n
Полученная система содержит n-1 уравнение. Применяем описанную выше процедуру к этой системе. Операции повторяем требуемое число раз, пока не приведем систему к треугольному виду:
x1+с12 x2+ . . .+с1n xn=с1n+1
c22 x2+ . . .+c2n xn=c2n+1
. . . .
cnn xn=cnn+1
Теперь легко определить xn,xn-1, . . ., x1. Если det(A)=0, то исходная система не имеет решений и процедура выдает S=0 иначе S=1 и решения находятся в массиве X.
Метод простых итераций заключается в итерационном вычислении значений по формуле:
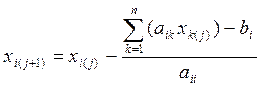 ,
до тех пор пока
,
до тех пор пока ![]()
где j- номер итерации, e – заданная погрешность вычислений. Итерационный процесс сходится, если величина модуля каждого диагонального элемента матрицы A больше суммы модулей остальных элементов. Начальные значения вектора X задаются пользователем.
Метод Зейделя подобен методу простых итераций, однако, уточненные значения сразу подставляются в последующие уравнения. Формула имеет вид:
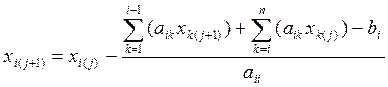 .
.
--------------------------------------------------------------------------------------------------------------------------
N 2
Разработать программу. Задана последовательность чисел, по требованию пользователя выполнить одно из следующих заданий:
a) найти разницу между средним арифметическим и средним геометрическим;
b) найти самую длинную подпоследовательность, упорядоченную по возрастанию;
c) поменять местами четные и нечетные (по порядку) элементы;
d) определить среднее арифметическое, отбросив предварительно минимальный и максимальный элементы.
--------------------------------------------------------------------------------------------------------------------------
N 3
Каждый год статистический центр региона оценивает загруженность профессорско-преподавательского состава всех подчиненных ему вузов. Эта оценка базируется на отчетах, представляемых преподавателями и содержащих данные о среднем количестве часов в неделю, отработанных ими в течение года. В результате этой оценки составляется таблица, в которой каждый преподаватель занимает определенное место, и определяется общее место вуза среди других учебных заведений.
Степень загруженности преподавателей определяется следующим образом:
e) преподаватель, отработавший более 55 часов в неделю, считается очень загруженным;
f) преподаватель, отработавший от 35 до 55 часов в неделю (включительно), считается загруженным удовлетворительно;
g) преподаватель, отработавший менее 35 часов в неделю, считается слабо загруженным.
Для определения загруженности каждого вуза сначала вычисляется средняя загруженность ее преподавательского состава, которая затем сравнивается с нормами, установленными правилами (а-с).
Разработать программу оценки загруженности преподавателей. Отчет выдавать как для одного учебного заведения, так и для всех.
-------------------------------------------------------------------------------------------------------------------------------
N 4
Разработать программу расчета основных статистических
характеристик реализации случайной величины: ![]() Требуется
найти такие характеристики, как начальный момент k-того порядка,
центральный момент k-того порядка, определить численно функцию плотности и
распределения вероятностей на j-ых интервалах. Расчет характеристик
осуществлять по выбору пользователя.
Требуется
найти такие характеристики, как начальный момент k-того порядка,
центральный момент k-того порядка, определить численно функцию плотности и
распределения вероятностей на j-ых интервалах. Расчет характеристик
осуществлять по выбору пользователя.![]()
-------------------------------------------------------------------------------------------------------------------------------
N 5
Разработать программу сглаживания данных по методу линейного сглаживания по трем точкам и по пяти точкам, методом нелинейного сглаживания по семи точкам. Метод выбирает пользователь.
Линейное сглаживание по трем точкам реализуется с помощью следующих
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.