Cети Петри. Структура СП. Гибкий производственный модуль. Алгоритм преобразования в ординарную СП, страница 2

 

                             или                3

p_j              t_i                       p_j         t_i 

Кратность входной позиции p_k - это число #(p_k;I(t_i)), которое показывает сколько раз позиция p_k встречается в множестве I(t_i),например: I(t₁)={p₁,p₁,p₁} - кратность равна 3.

Кратность выходной позиции p_k - это аналогичное число #(p_k,O(t_i)).

Петля - это контур, состоящий из одной и той же позиции p_k для события t_i.                       

 

         p_k                       p_k              t_i 

 

         t_i

Чистая СП - это СП свободная от петель(А).

 

A).       p₂           t₂             p₃

3

t₁

          p₁                    t₃

Б).                 p₁

 

                t₁                              t₂      {(p₂,t₃),(t₃,p₂)}

- петля

p₂                                      p₃

 

t₃

t₃

Ординарная СП - это СП, не имеющая кратных дуг (н-р, Б).

Утверждение 1: Любая маркированная СП может быть преобразована в маркированную ординарную СП без петель.

     Алгоритм преобразования в ординарную СП

1. Для всех p_kÎP определяется

n(p_k) = max (#(p_k,I(t_i))+#(p_k,(O(t_i))).

                           ^t_i ^{Î T}

 

2. Определяется множество дополнительных позиций P`:

_n                      p_k, если n(p_k)=1

P`= È P`(p_k), где P`(p_k)= { (p_k,1,p_k,2,...,p_k,n(pk)),

^k=1                     если n(p_k) ³ 2 

_n  

½P`½ =  S  n(p_k).

^k=1

3. Объявляются “нормальные переходы” - T={t₁,t₂,...,t_m}.

4. Определяются “кольцевые переходы” для всех n(p_k)³2:

T`(p_k)={r_k,1,r_k,2,...,r_k,n(pk)},

_n

T`= T È ( È T`(p_k)).

^k=1 

5. Для каждого p_k c n(p_k)³2 образуется “кольцевая” подсеть:

r_k,n(pk)    p_k,1     r_k,1      p_k,2

                     

 

p_k,n(pk)                                               r_k,2

 

p_k,3

r_k,3

p_k,4

6. Каждый “нормальный” переход t_iÎT связывается с соответствующими позициями p_k(для n(p_k)=1) и позициями (p_k,1,p_k,2,...,p_k<n(pk))(для n(p_k)³2) согласно тем связям, которые имелись в сети С, лишь бы не возникали ситуации, когда переход t_i и позиция p_k,i связаны более, чем одной дугой.

7. Производится начальная разметка СП:

m₀`(p_k)= m₀(p_k), если n(p_k)=1

m₀`(p<sub>k,1</sub>)= m<sub>0</sub>(p<sub>k</sub>) и  m<sub>0</sub>`(p_k,i)=0, для i=[2,n(p_k)].

Пример 2: Пусть дана чистая СП(А):  T={t₁,t₂,t₃}

P={p₁,p₂,p₃}

m₀=(2,0,0)

1. n(p₁)=max (#(p₁,I(t_i)+#(p₁,O(t_i)))= max(0+1, 0+1, 2+0)=2

^{tiÎT                               t1     t2     t3}

n(p₂)=max(1+0, 1+0)= 1

                    ^{t1     t2}

n(p₃)= max(0+3, 0+1)= 3

                     ^{t2     t3}

  

2. P`(p₁)={p_1,1, p_1,2}

P`(p₂)={p₂}

P`(p₃)={p_3,1, p_3,2, p_3,3}

3. Установка “нормальных” переходов:

        t₁                 t₂                 t₃

 

 

4-5. Построение кольцевых подсетей:

                         r_1,2   

                     

p₁:    p_1,1                  p_1,2      T`(p₁)={r_1,1,r_1,2}

r_1,1

 

 

 

                     r_3,1       r_3,2

p_3,1       p_3,2        p_3,3

p₃:

Т’(p₃)={r_3,1,r_3,2,r_3,3,}

r_3,3

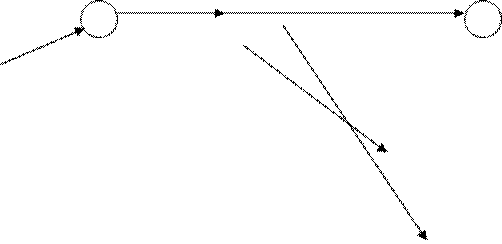
6-7. Построение ординарной сети: 

                p₂          t₂                p_3,1   

 

     t₁                                   r_3,1

r_1,2                    

p_3,2

    p_1,1                   p_1,2      r_3,2       

 

r_1,1                      p_3,3

t₃                      r_3,3

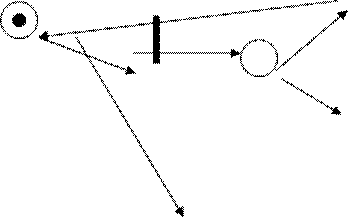
            Автоматные сети

Автоматная СП - это ординарная СП, в которой каждый переход имеет ровно одну входную и одну выходную позиции.

 

 

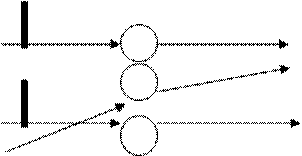
Маркированный граф

Маркированный граф или синхрограф - это ординарная СП, в которой каждая позиция имеет один входной и один выходной переход.