Лабораторная работа
«ИСПОЛЬЗОВАНИЕ ФУРЬЕ-ПРЕОБРАЗОВАНИЯ В СИСТЕМАХ ОПТИЧЕСКОЙ ОБРАБОТКИ ИНФОРМАЦИИ А»
Цель работы: Знакомство с оптическим фурье-преобразованием и пространственной фильтрацией фурье-спектра изображения.
Объекты исследования: Экспериментальная установка, осуществляющая фурье-преобразование волнового поля объекта и пространственную фильтрацию его фурье-спектра. Штриховая мира, используемая в установке в качестве объекта.
Задачи, решаемые в работе:
1. Ознакомиться с установкой осуществляющей оптическое фурье-преобразование по схеме 4F.
2. Ознакомиться с влиянием пространственной фильтрации фурье-спектра штриховой миры на качество её изображения.
3. Измерить распределение максимумов интенсивности фурье-спектра штриховой миры.
4. Рассчитать распределение максимумов интенсивности фурье-спектра штриховой миры. Сравнить расчётные и измеренные значения.
Любая световая волна, распространяющаяся
в свободном пространстве, может быть представлена в виде суперпозиции плоских
волн. Математически это выражается в том, что комплексная амплитуда
монохроматической световой волны ![]() , где
, где ![]() -радиус-вектор точки
пространства, представляется в виде суперпозиции комплексных амплитуд плоских
волн
-радиус-вектор точки
пространства, представляется в виде суперпозиции комплексных амплитуд плоских
волн
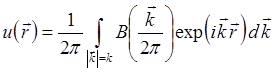 ,
(1)
,
(1)
где ![]() комплексная
амплитуда плоской волны,
комплексная
амплитуда плоской волны, ![]() -волновой
вектор плоской волны,
-волновой
вектор плоской волны, 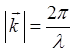 -волновое число,
-волновое число, ![]() -длина волны света,
интегрирование выполняется по сфере радиуса
-длина волны света,
интегрирование выполняется по сфере радиуса ![]() .
.
В выражение (1) входит коэффициент 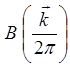 с которым разные плоские
компоненты входят в данную суперпозицию. Он определяется следующим выражением
с которым разные плоские
компоненты входят в данную суперпозицию. Он определяется следующим выражением
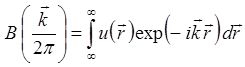 . (2)
. (2)
Математически выражения (1) и (2)
представляют собой обратное и прямое преобразования Фурье, соответственно.
Функция 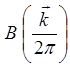 называется преобразованием
Фурье или фурье-образом (иначе спектром Фурье или частотным спектром)
комплексной функции
называется преобразованием
Фурье или фурье-образом (иначе спектром Фурье или частотным спектром)
комплексной функции ![]() . Таким образом,
представление световой волны в виде суперпозиции плоских волн эквивалентно
нахождению фурье-образа комплексной амплитуды волны
. Таким образом,
представление световой волны в виде суперпозиции плоских волн эквивалентно
нахождению фурье-образа комплексной амплитуды волны ![]() .
.
В оптике преобразование Фурье
осуществляется с помощью линзы. Волновое поле в задней фокальной плоскости
положительной линзы представляет собой фурье-образ волнового поля в её передней
фокальной плоскости. При установке в передней фокальной плоскости линзы
транспаранта с амплитудным пропусканием ![]() и
освещении транспаранта плоской волной, падающей по нормали, в задней фокальной
плоскости линзы возникает фурье-образ транспаранта
и
освещении транспаранта плоской волной, падающей по нормали, в задней фокальной
плоскости линзы возникает фурье-образ транспаранта
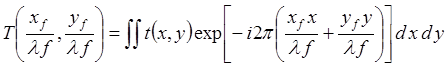 ,
(3)
,
(3)
где ![]() -длина
волны света,
-длина
волны света, ![]() -фокусное расстояние линзы,
-фокусное расстояние линзы, ![]() -координаты в фокальной
плоскости линзы. Аргументы
-координаты в фокальной
плоскости линзы. Аргументы ![]() ,
, ![]() фурье-образа
фурье-образа 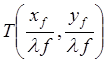 имеют физический смысл
пространственных частот
имеют физический смысл
пространственных частот ![]() ,
,![]() амплитудного пропускания
транспаранта
амплитудного пропускания
транспаранта ![]() по координатам
по координатам ![]() ,
,![]() ,
соответственно. Согласно (3) амплитуда и фаза световой волны в точке фокальной
плоскости линзы с координатами
,
соответственно. Согласно (3) амплитуда и фаза световой волны в точке фокальной
плоскости линзы с координатами ![]() равна
амплитуде и фазе спектра амплитудного пропускания транспаранта на
пространственных частотах
равна
амплитуде и фазе спектра амплитудного пропускания транспаранта на
пространственных частотах 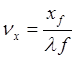 ,
, 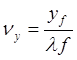 . Из (3) также следует, что в
точку фокальной плоскости линзы с координатами
. Из (3) также следует, что в
точку фокальной плоскости линзы с координатами ![]() фокусируется
плоская волна из суперпозиции плоских волн (1), с компонентами
фокусируется
плоская волна из суперпозиции плоских волн (1), с компонентами 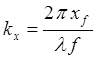 ,
, 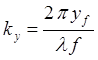 волнового
вектора
волнового
вектора ![]() . Если транспарант сместить из
передней фокальной плоскости линзы, то это никак не повлияет на интенсивность
волнового поля в задней фокальной плоскости линзы, изменится только его фаза,
которая будет отличаться от фазы фурье-образа.
. Если транспарант сместить из
передней фокальной плоскости линзы, то это никак не повлияет на интенсивность
волнового поля в задней фокальной плоскости линзы, изменится только его фаза,
которая будет отличаться от фазы фурье-образа.
Если за первой линзой установить вторую
линзу, так чтобы её передняя фокальная плоскость совпадала с задней фокальной
плоскостью первой линзы, то она выполнит второе фурье-преобразование. Два
последовательных фурье-преобразования дают исходную функцию, с точностью до
изменения знаков координат по осям ![]() на
обратные. В результате в задней фокальной плоскости второй линзы возникнет
перевёрнутое на 180 градусов вокруг осей
на
обратные. В результате в задней фокальной плоскости второй линзы возникнет
перевёрнутое на 180 градусов вокруг осей ![]() изображение
объекта, установленного в передней фокальной плоскости первой линзы.
изображение
объекта, установленного в передней фокальной плоскости первой линзы.
Экспериментальная установка, осуществляющая оптическое фурье-преобразование и пространственную фильтрацию фурье-спектра штриховой миры имеет cхему представленнyю на рис. 1.
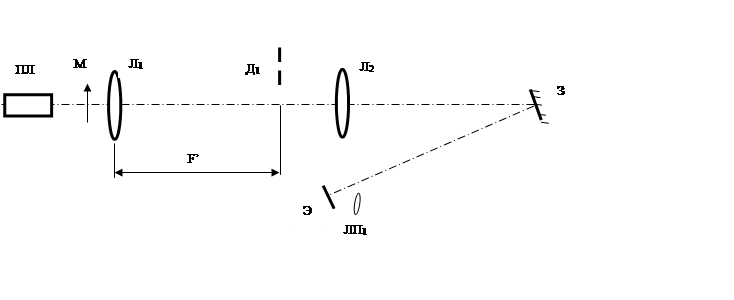 |
Рис. 1
Установка содержит следующие узлы, располагаемые в соответствии со схемой на рис.1:
1. Полупроводниковый лазер ПЛ.
2. Штриховую миру М
3. Линзу Л1
4. Линзу Л2
5. Зеркало З
6. Экран Э
7. Лупу на рейтере ЛП1
8. Лупу ЛП2
9. Диафрагму Д1 с круглым отверстие диаметром 0,5 мм
11. Фотодиод ФД-24К
12. Милливольтметр
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.