Основные понятия и определения. Эйлеровы графы. Гамильтоновы графы. Свойства гамильтоновых графов. Теория трансверсалей

обладающих тем свойством, что никакие два из них не имеют общих ребер. Девять гурманов проводят каждый вечер в своем любимом ресторане в течение всей конференции. Предположим, что они садятся за круглый стол, причем любые двое из них занимают соседние места только один раз. Что можно сказать о продолжительности конференции? Выполните первое задание упражнения для двудольного графа  и найдите аналогичное «практическое» приложение этого случая.

13.  Докажите, что существует ровно шесть неизоморфных деревьев с шестью вершинами и одиннадцать — с семью вершинами.

14.  Докажите, что каждое дерево является двудольным графом; какие деревья являются полными двудольными графами?

15.  Найдите остовное дерево и ассоциированные с ним фундаментальные системы циклов и разрезов следующих графов: a) ; б) ; в) ; г) ; д) Платоновых графов; е) графа Петерсена.

16.  Пусть А — матрица инциденций дерева с  вершинами. Докажите, что любые  столбцов матрицы А линейно независимы над полем целых чисел по модулю 2.

17.  Найдите какой-нибудь другой алгоритм для решения задачи о соединении городов, включающий удаление из графа G ребер самой большой меры. Покажите, что если меры всех ребер совпадают, то этот алгоритм дает метод построения остовного дерева графа G.

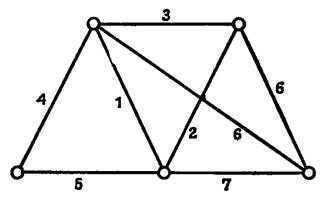
18.  Найдите остовное дерево с минимально возможной суммой мер для графа, изображенного на рисунке.

19.  Пусть G — многогранник (или граф многогранника), все грани которого ограничены пятиугольниками и шестиугольниками; что можно сказать о числе пятиугольных граней? Докажите, что если в каждой вершине сходятся в точности три грани, то число пятиугольных граней должно равняться двенадцати.

20.  Пусть G — плоский граф с числом граней, меньшим двенадцати. Покажите, что если степень любой вершины из G не меньше трех, то в G существует грань, ограниченная самое большее четырьмя ребрами.

21.  Найдите хроматические числа Платоновых графов. Что можно сказать о хроматических числах а) соединения двух графов; б) объединения двух графов?

22.  Пусть G — простой граф с  вершинами, являющийся регулярным степени ; покажите, что .

23.  Граф называется критическим, если удаление любой из его вершин (вместе с инцидентными ей ребрами) приводит к графу с меньшим хроматическим числом. Покажите, что а)  является критическим для всех ; б)  является критическим тогда и только тогда, когда  нечетно. Покажите также, что если  нечетно, то соединение  является критическим графом, хроматическое число которого равно шести.

24.  Разобьем плоскость на конечное число областей, проводя бесконечные прямые линии произвольным образом. Докажите (тремя различными способами), что эти области допускают 2-раскраску.

25.  Пусть D — простой орграф с  вершинами и  дугами; покажите, что если D связен, но не сильно связен, то , а если D сильно связен, то .

26.  Пусть D — орграф; для любых двух вершин  и  положим  тогда и только тогда, когда существует простая орцепь из  в  Покажите, что отношение  является частичным упорядочением в том и только в том случае, если D не содержит орциклов. Как можно было бы охарактеризовать сильно связный орграф на языке отношения ?

27.  Обратный к D орграф получается из D переменной направления каждой дуги орграфа D. Приведите пример орграфа D, изоморфного своему обратному. Что можно сказать о матрицах смежности орграфа и обратного к нему орграфа?

28.  Пусть А — матрица смежности орграфа с множеством вершин . Докажите, что ()-му элемент из  равен числу ориентированных маршрутов длины  из  в . Какой смысл можно придать суммам строк и суммам столбцов матрицы А?

29.  Три миссионера и три людоеда находятся на одном берегу реки, через которую им надо переправиться; к несчастью, их лодка выдерживает только двух человек, и если все миссионеры умеют грести, из людоедов на это способен только один. Используя результат предыдущего упражнения, найдите, сколько