Вычисления с приближенными числами. Практическая оценка погрешности результатов вычислений

ЛАБОРАТОРНЫЕ РАБОТЫ В СИСТЕМЕ MATHCAD

Лабораторная работа 1

Вычисления с приближенными числами

Цель: научиться практически оценивать погрешности результатов вычислений.

Краткие теоретические сведения

Перед выполнением работы изучите материал гл. 1, ответьте        на вопросы и выполните задания для самоконтроля.

Рассмотрим пример определения погрешности.

Пример. Погрешности арифметических действий.

Пусть числа х и у заданы с абсолютными погрешностями              и :

Тогда относительные погрешности чисел:

Найдем погрешности суммы и разности чисел:

Задания

1. Величина подъемной силы крыла самолета оценивается по формуле , где с – коэффициент, зависящий от формы крыла;  – угол атаки, отсчитываемый от направления нулевой              подъемной силы;  – плотность атмосферы на заданной высоте;                  v – скорость натекания воздуха на крыло; – площадь проекции крыла на горизонтальную плоскость. Требуется вычислить  и                   при заданных значениях с, , , v,и заданных абсолютных и относительных погрешностях этих величин. Результат запишите с сохранением только верных значащих цифр. Исходные данные приведены в таблице (для нечетных вариантов задано  и , для четных               и ):

Вариант	с						v	или		или
1	0,005	0,001	15	0,01	0,99	0,01	200	3	20	0,001
2	0,004	0,001	15	0,01	0,98	0,01	170	0,01	20	0,04
3	0,005	0,001	15	0,01	0,99	0,01	200	2	20	0,001
4	0,004	0,001	15	0,01	0,98	0,01	190	0,01	20	0,02
5	0,005	0,001	12	0,01	0,99	0,01	200	3	20	0,001
6	0,004	0,001	10	0,01	0,98	0,01	195	0,01	20	0,04
7	0,005	0,001	15	0,01	0,99	0,01	200	2	15	0,001
8	0,004	0,001	12	0,01	0,98	0,01	205	0,01	15	0,02
9	0,005	0,001	10	0,01	0,99	0,01	200	3	15	0,001
10	0,004	0,001	15	0,01	0,96	0,01	210	0,01	20	0,04
11	0,005	0,001	15	0,01	0,95	0,01	200	3	20	0,001
12	0,004	0,001	15	0,01	0,95	0,01	215	0,01	20	0,02
13	0,005	0,001	15	0,01	0,95	0,01	200	2	20	0,001
14	0,004	0,001	15	0,01	0,95	0,01	220	0,01	20	0,04
15	0,005	0,001	12	0,01	0,95	0,01	200	3	20	0,001
16	0,004	0,001	10	0,01	0,95	0,01	225	0,01	20	0,02
17	0,005	0,001	15	0,01	0,95	0,01	200	2	15	0,001
18	0,004	0,001	12	0,01	0,95	0,01	210	0,01	15	0,04
19	0,005	0,001	10	0,01	0,95	0,01	200	3	15	0,001
20	0,004	0,001	15	0,01	0,95	0,01	200	0,01	20	0,02

2. Найдите абсолютную и относительную погрешности вычисления функции при заданных значениях аргумента. Функции и приближенные значения аргументов приведены в таблице:

ПРАКТИЧЕСКИ ВЕЗДЕ РИСУНКИ ВМЕСТО ФОРМУЛ

Вариант	Функция	Аргументы
1
2
3		j0 » 3,147 ± 0,001
4
5
6
7
8
9
10
11
12

Окончание таблицы

Вариант	Функция	Аргументы
13
14
15
16
17
18
19
20

3. Получите формулы для оценки абсолютной погрешности функции двумя способами: а) используя формулы для абсолютных погрешностей арифметических операций; б) используя формулу для абсолютной погрешности функции многих переменных. Функции приведены в таблице:

Окончание таблицы

Пояснения. В качестве примера получим формулы для  определения абсолютной погрешности функции: .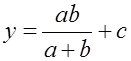

а) с помощью формул для абсолютных погрешностей арифметических операций:

, ,

,

.

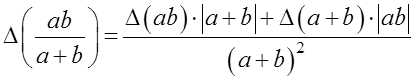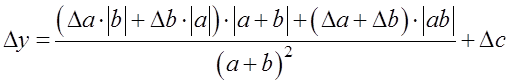б) используя формулу для абсолютной погрешности функции многих переменных:

 

, , .

.

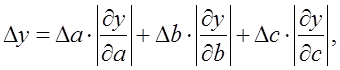
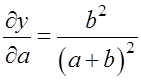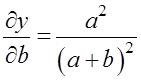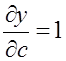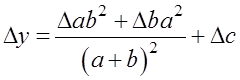Содержание отчета

Отчет о выполнении работы состоит из двух частей: теоретической и практической. В первой части отчета необходимо дать краткое описание использованных методов (привести рабочую формулу, геометрическую интерпретацию). Во второй части отчета должны быть представлены результаты выполнения практических заданий с текстами программ, анализ результатов и выводы.

Лабораторная работа 2

Численные методы решения нелинейных уравнений

Цель: изучить численные методы решения нелинейных уравнений с одним неизвестным; научиться программировать алгоритмы итерационных методов уточнения корней; сравнить скорость сходимости различных методов.

Краткие теоретические сведения

Перед выполнением работы рекомендуется внимательно изучить материал гл. 2, а также ответьте на вопросы и выполните задания для самоконтроля. Расчетные программы заданий 2–6 могут быть составлены на любом алгоритмическом языке (Бейсик, Паскаль, Си, Фортран).

Рассмотрим примеры решения нелинейных уравнений методами бисекций, простой итерации, Ньютона.

Пример 1. Локализация корней.

Рассмотрим уравнение

Построим в системе MathCAD его графики на различных интервалах:

Получили два отрезка локализации:

Тогда в первом случае простой корень будет на отрезке               [–0,6; –0,4], а во втором – кратный корень на отрезке [–0,2; 0,2].

Пример 2. Решение уравнения методом бисекции.

Рассмотрим уравнения  из первого примера. Вводим данное уравнение в систему MathCAD.

Пример 3. Решение уравнения методом Ньютона.

Используем то же уравнение, что и в предыдущих примерах:

Метод Ньютона в системе MathCAD будет выглядеть следующим образом:

Введем начальные значения:

Пример 4. Чувствительность метода Ньютона к выбору начального приближения.

Рассмотрим уравнение .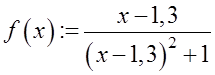

Очевидно, что корень равен 1,3 по методу Ньютона:

Задания

1. Графическим методом определите наличие, приблизительное расположение