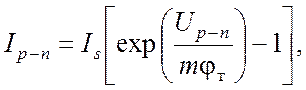 (2)
(2)
где Is – тепловой ток насыщения p-n-перехода, неизменный для данной температуры; m – коэффициент, определяемый свойствами конкретного p-n-перехода (его значения изменяются от 1 до нескольких единиц); φт – тепловой (температурный) потенциал. Зависимость φт от температуры описывается выражением
![]()
где k = 1,38·10-23 Дж/К – постоянная Больцмана; T – абсолютная температура, К; е = 1,6·10-19 Кл – заряд электрона.
При нормальной температуре (T = 300 К) φт ≈ 0,026 В.
Таким образом, нашей задачей является определение неизвестных пока параметров нелинейной модели диода rб, rут, Is и m.
Сопротивление утечки rут определяется так же, как и для кусочно-линейной модели диода.
Параметры rб и m определяются по прямой ветви ВАХ с помощью так называемого метода выравнивания характеристик. Суть метода заключается в том, что нелинейная зависимость I = f (U), описываемая нелинейным уравнением, заменяется эквивалентной линейной зависимостью в новой системе координат (назовем их условно x и y). Эта эквивалентная зависимость описывается классическим уравнением прямой y= b+ kx с легко определяемыми параметрами b и k. Найдя эти параметры, можно перейти к исходному нелинейному уравнению и определить его коэффициенты.
Проиллюстрируем данный метод на примере – найдем параметры нелинейной модели диода (рис. 3), прямая ветвь ВАХ которого представлена на рис. 4.
Уравнение (2) можно переписать в виде
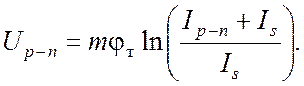 (3)
(3)
С учетом выражения (3) внешнее напряжение на диоде Uд можно связать с его током Iд следующим соотношением:
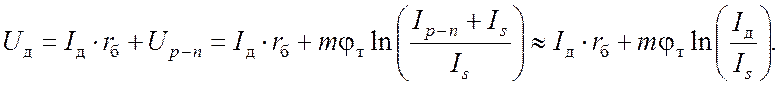 (4)
(4)
Показанное в выражении (4) упрощение возможно лишь в случае включения диода в прямом направлении, когда тепловым током насыщения Is и током утечки Iут можно пренебречь по сравнению с током p-n-перехода Ip-n (он превышает их на несколько порядков величины). Поэтому и можно считать, что Iд = Ip-n + Iут ≈ Ip-n, а Ip-n + Is ≈ Ip-n ≈ Iд.
|
|
Рис. 4. К определению параметров нелинейной модели диода по прямой ветви его вольт-амперной характеристики |
Найти параметры rб и m
можно, вспомнив, как определяется понятие дифференциального сопротивления – ![]() . Если имеется графическая
зависимость I = f (U) (ВАХ), дифференциальное
сопротивление можно определить по наклону касательной, проведенной к этой ВАХ в
какой-либо ее точке. Очевидно, что при нелинейном характере зависимости I = f (U), характерном для диода,
значение rдиф будет
различно для различных точек этой зависимости.
. Если имеется графическая
зависимость I = f (U) (ВАХ), дифференциальное
сопротивление можно определить по наклону касательной, проведенной к этой ВАХ в
какой-либо ее точке. Очевидно, что при нелинейном характере зависимости I = f (U), характерном для диода,
значение rдиф будет
различно для различных точек этой зависимости.
Найдем выражение для дифференциального сопротивления диода, взяв производную от правой части выражения (4) по току Iд:
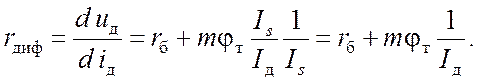 (5)
(5)
Если представить, что rдиф – это зависимая
переменная, а величина ![]() – независимая
переменная, то графиком функции
– независимая
переменная, то графиком функции ![]() будет прямая.
Действительно, уравнение (5) является по сути уравнением прямой вида y= b+ kx, где y = rдиф,
будет прямая.
Действительно, уравнение (5) является по сути уравнением прямой вида y= b+ kx, где y = rдиф, ![]() , а величины rб и mφт – коэффициенты b
и k
соответственно. Именно эти коэффициенты
мы и будем искать.
, а величины rб и mφт – коэффициенты b
и k
соответственно. Именно эти коэффициенты
мы и будем искать.
Так как графиком функции y= b+ kx является прямая, для его построения достаточно найти две принадлежащие этой прямой точки. Отметим на прямой ветви вольт-амперной характеристики диода две произвольные точки 1 и 2 (рис. 4). Для большей точности определения параметров rб и mφт точки следует выбирать на участках ВАХ, имеющих значительно отличающуюся крутизну. Проведем через эти точки две касательные к характеристике. Значения дифференциальных сопротивлений определяются как котангенсы углов наклона этих касательных (при этом необходимо учитывать различие масштабов по осям тока и напряжения), но можно поступить и так, как мы определяли rпр в кусочно-линейной модели диода. Величину rдиф можно найти как отношение длин катетов прямоугольного треугольника, гипотенузой которого является проведенная касательная (рис. 4):
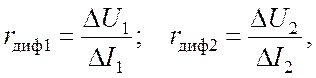
где rдиф1, rдиф2 – значения дифференциального сопротивления диода в точках 1 и 2 соответственно.
Для показанной на рис. 4 характеристики
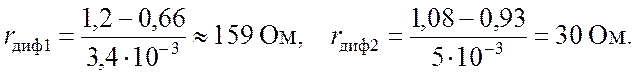
Величины ![]() для
выбранных точек 1 и 2 составляют
для
выбранных точек 1 и 2 составляют
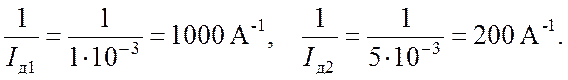
Построим зависимость (5) в системе
координат ![]() . Для этого отметим две точки
(назовем их условно 1’ и 2’) с найденными только что координатами
. Для этого отметим две точки
(назовем их условно 1’ и 2’) с найденными только что координатами
![]() ,
, ![]() и
соединим их прямой (рис. 5). Точка пересечения этой прямой с осью rдиф определяет значение rб. Действительно, когда
второе слагаемое в выражении (5) обращается в ноль, т.е. когда
и
соединим их прямой (рис. 5). Точка пересечения этой прямой с осью rдиф определяет значение rб. Действительно, когда
второе слагаемое в выражении (5) обращается в ноль, т.е. когда ![]() = 0 и мы находимся на оси rдиф, rдиф = rб. Для показанной на
рис. 5 зависимости rб ≈ 2
Ом.
= 0 и мы находимся на оси rдиф, rдиф = rб. Для показанной на
рис. 5 зависимости rб ≈ 2
Ом.
Значение произведения mφт в соответствии с выражением (5), являющимся для
системы координат ![]() уравнением прямой, найдем
по отношению разности координат двух точек на этой прямой. Удобнее использовать
уже известные нам координаты точек 1’ и 2’. Тогда
уравнением прямой, найдем
по отношению разности координат двух точек на этой прямой. Удобнее использовать
уже известные нам координаты точек 1’ и 2’. Тогда
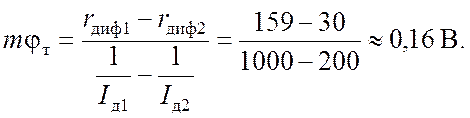
Зная величину φт для данной температуры, можно отдельно найти значение коэффициента m. Например, в нашем случае при T = 293 К, когда φт ≈ 0,025 В, m = 0,16/0,025 = 6,4.
|
|
Рис. 5. Зависимость rдиф = f (1/Iд), соответствующая вольт-амперной характеристике диода, приведенной на рис. 4 |
Значение теплового тока насыщения p-n-перехода Is найдем, преобразовав выражение (2) и подставив в него координаты произвольной точки на ВАХ диода (например, точки 2) и найденные параметры rб и mφт. При этом, исходя из нелинейной модели диода (рис. 3), в качестве напряжения на p-n-переходе Up-n мы будем подставлять разность внешнего напряжения на диоде Uд и падения напряжения на сопротивлении rб:
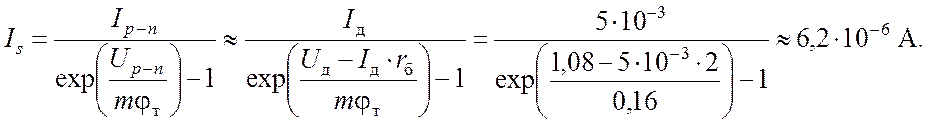
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.