



























































Оптимальные смешанные стратегии в игре с матрицей, полученной усечением исходной за счет доминируемых строк и столбцов, дадут оптимальное решение в исходной игре: доминируемые чистые стратегии игроков в смешении не участвуют – соответствующие им вероятности следует взять равными нулю.
Рассмотрим игру ![]() , а также все выпуклые комбинации
строк матрицы А.
, а также все выпуклые комбинации
строк матрицы А.
1-я выпуклая комбинация:
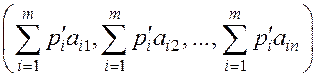 ,
,
![]() ,
, ![]() ;
;
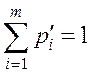 .
.
2-я выпуклая комбинация:
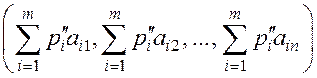 ,
,
![]() ,
, ![]() ;
;
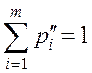 .
.
Если для этих комбинаций выполняются неравенства
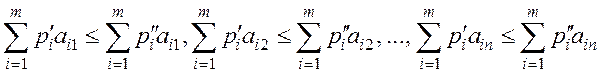 , то
говорят, что первая комбинация доминирует над второй, а вторая доминируется
первой. И тогда первая комбинация называется доминируемой, а вторая – доминирующей.
, то
говорят, что первая комбинация доминирует над второй, а вторая доминируется
первой. И тогда первая комбинация называется доминируемой, а вторая – доминирующей.
Рассмотрим две выпуклые комбинации столбцов матрицы А.
1-я выпуклая комбинация:
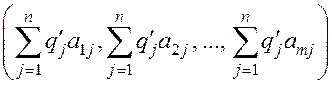 ,
,
![]() ,
, ![]() ;
;
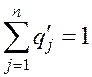 .
.
2-я выпуклая комбинация:
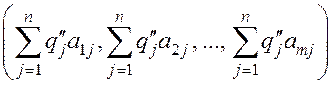 ,
, ![]() ,
,
![]() ;
; 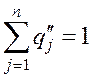 .
.
Если для этих комбинаций выполняются неравенства
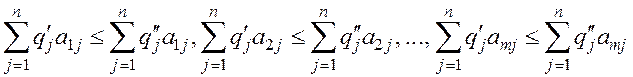 , то говорят, что вторая комбинация доминирует
над первой, а первая доминируется второй. И тогда вторая комбинация называется
доминируемой, а первая – доминирующей.
, то говорят, что вторая комбинация доминирует
над первой, а первая доминируется второй. И тогда вторая комбинация называется
доминируемой, а первая – доминирующей.
Если в неравенствах стоит строгий знак неравенства, то это есть пример строгого доминирования одной выпуклой комбинации над другой.
Если в неравенствах стоит нестрогий знак, то это пример нестрогого доминирования.
Если в неравенствах может быть поставлен знак равенства, то выпуклые комбинации будут называться дублирующими.
Справедливы следующие предложения.
1. Если над k-й строкой ![]() матрицы игры доминирует некоторая
выпуклая комбинация остальных ее строк, то существует такая оптимальная
смешанная стратегия игрока А, в которой вероятность выбора чистой k-й стратегии равна нулю.
матрицы игры доминирует некоторая
выпуклая комбинация остальных ее строк, то существует такая оптимальная
смешанная стратегия игрока А, в которой вероятность выбора чистой k-й стратегии равна нулю.
2. Если над r-м столбцом матрицы игры доминирует некоторая выпуклая комбинация остальных ее столбцов, то тогда существует такая смешанная стратегия игрока В, в которой вероятность выбора r-й стратегии игрока В равна нулю.
3. Если существуют доминируемые стратегии игроков, то с позиции оптимального поведения от данных стратегий можно избавиться.
4. Если существуют дублирующие стратегии (дублирующие выпуклые комбинации), то тогда все их кроме одной можно удалить из рассмотрения.
Замечание 8. Матрицу игры, имеющую решение в чистых стратегиях, можно редуцировать (сократить по принципу доминирования) до седлового элемента.
Пример 8. Удаляя доминируемые и дублирующие стратегии игроков, произведем редуцирование матрицы игры
![]()
![]()
![]()
![]()
![]()
![]()
![]()
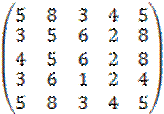
Решение:
1)рассмотрим стратегии А1 и А5 – дублирующие, убираем А5;
2) рассмотрим стратегии А2 и А3: А3 – доминирующая стратегия, А2 – доминируемая, убираем ее;
3) рассмотрим стратегии А1 и А4: А1 – доминирующая, А4 – доминируемая стратегия, вычеркиваем ее;
4) рассмотрим стратегии В1 и В2: В1 – доминирующая, В2 – доминируемая, вычеркиваем ее;
5) рассмотрим стратегии В4 и В5: В4 – доминирующая, В5 – доминируемая стратегия, вычеркиваем ее;
6) рассмотрим стратегии В1 и В4: В4 – доминирующая, В1 – доминируемая стратегия, вычеркиваем ее.
Получаем матрицу игры 2 × 2: 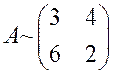 .
.
Пример 9. Применим доминирование, найдем нижнюю и верхнюю цены
игры и седловой элемент 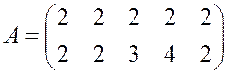 .
.
Решение: Имеется решение в чистых стратегиях ![]() ,
а25, а21, а22 – седловой
элемент. Применим принцип доминирования
и сократим искомую матрицу:
,
а25, а21, а22 – седловой
элемент. Применим принцип доминирования
и сократим искомую матрицу:
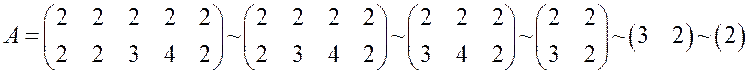 .
.
Вопросы и задания для самоконтроля
1. Каким образом можно уменьшить размерность платежной матрицы?
2. Дайте определение доминирующей стратегии для игрока А.
3. Какая стратегия игрока В называется доминируемой?
4. Дайте определение дублирующих стратегий игрока и объясните, почему одну из дублирующих стратегий можно удалить.
Задания для самостоятельного решения
1. Используя правило доминирования, уменьшите размерность матриц, найдите нижнюю цену игры, верхнюю цену игры, определите седловые точки, оптимальные чистые стратегии и цену игры (если они существуют).
1. 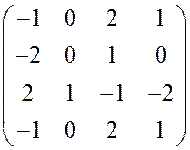 . 2.
. 2. 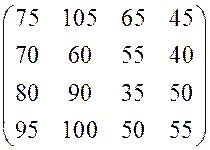 .
.
3. 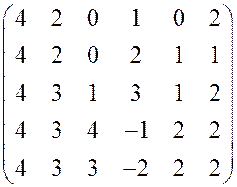 . 4.
. 4. 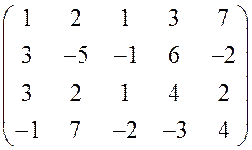 .
.
5. 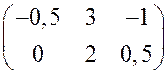 . 6.
. 6. 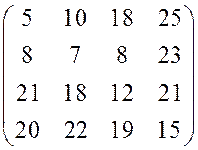 .
.
7. 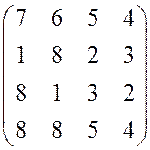 . 8.
. 8. 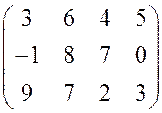 . 9.
. 9. 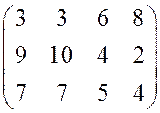 .
.
10. Докажите на примере, что доминируемая чистая стратегия не может быть оптимальной.
2.5. Графический метод решения игр
Решить игру – означает найти цену игры и оптимальные стратегии. Рассмотрение методов нахождения оптимальных смешанных стратегий для матричных игр начнем с простейшей игры, описываемой матрицей 2 × 2.
Пусть имеется платежная матрица 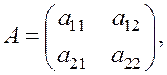 при этом
при этом
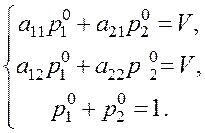
Приравняем первое и второе равенства, тогда
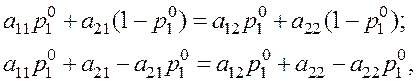
откуда получаем оптимальные значения ![]() и
и
![]() :
:
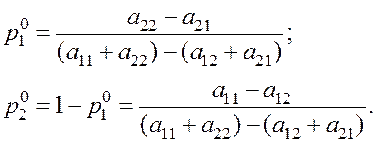
Цена игры будет найдена по формуле
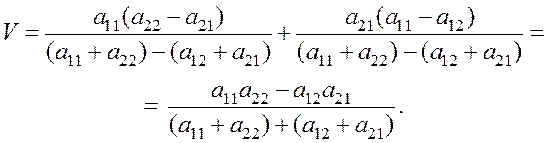
Вычислив V, находим ![]() и
и ![]() :
:
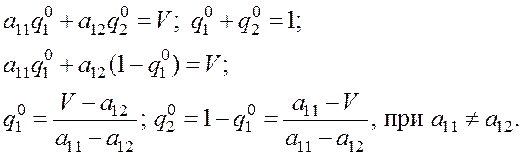
Задача решена, так как найдены векторы ![]() и цена игры V.
и цена игры V.
Пример 2.10. Найти решение игры 2 × 2 аналитически (табл. 2.6).
Таблица 2.6
|
Вj |
||
|
Ai |
В1 |
В2 |
|
А1 |
–2 |
4 |
|
А2 |
5 |
–3 |
Решение. Определим наличие решения в чистых стратегиях (табл. 2.7):
![]()
Таблица 2.7
|
Вj |
|||
|
Ai |
В1 |
В2 |
αi |
|
А1 |
–2 |
4 |
–2 |
|
А2 |
5 |
–3 |
–3 |
|
βj |
5 |
4 |
|
Найдем решение игры в смешанных стратегиях.
Р0 = (р1; р2);
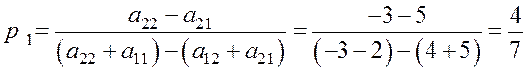 .
.
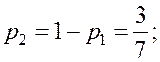
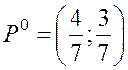 – оптимальная смешанная
стратегия игрока А;
– оптимальная смешанная
стратегия игрока А;
Q0 = (q1; q2);
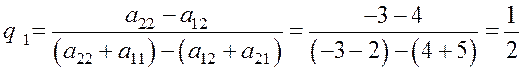 .
.
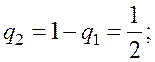 .
.
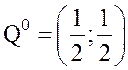 – оптимальная смешанная стратегия
игрока В;
– оптимальная смешанная стратегия
игрока В;
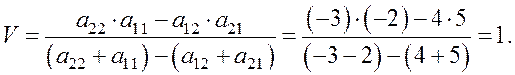
Имея матрицу платежей А, можно решить задачу графически.
Алгоритм нахождения решения следующий.
1. По оси абсцисс откладывается отрезок единичной длины.
2. По оси ординат откладываются выигрыши при стратегии А1.
3. На линии, параллельной оси ординат, в точке 1 откладываются выигрыши при стратегии А2.
4. Концы отрезков обозначаются для a11, a12, a22, a21 и проводятся две прямые линии a11a12 и a21a22.
5. C позиции максиминного поведения игрок А выберет нижнюю огибающую
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.