Сибирский Государственный Университет Телекоммуникаций и Информатики
Хабаровский Филиал
Функции нескольких переменных, кратные и криволинейные интегралы (конспект лекций)
Хабаровск 2003г.
А.Н.: Функции нескольких переменных, кратные и криволинейные интегралы, теория поля (конспект лекций).
Конспект лекций предназначен для студентов факультета заочного обучения и рассматривает все вопросы по темам: функции нескольких переменных, кратные и криволинейные интегралы, теория поля. Приведено подробное решение примеров по всем темам. Кроме того, даны примеры для самостоятельного решения.
факультета дневного отделения от 5.03.2003г
3
1.1 Функции двух и многих переменных. Основные понятия
Определение.
Величина ![]() называется
функцией переменных величин
называется
функцией переменных величин ![]() и
и
![]() на
множестве
на
множестве ![]() ,
если каждой точке этого множества соответствует одно или несколько определенных
значений величины
,
если каждой точке этого множества соответствует одно или несколько определенных
значений величины ![]() :
:
![]()
Множество точек ![]() называется
областью определения функции
называется
областью определения функции ![]() .
.
Аналогично можно определить функцию многих независимых переменных:
![]()
Определение. Число ![]() называется
пределом функции
называется
пределом функции ![]() при
при
![]() ,
если для всех значений
,
если для всех значений ![]() и
и
![]() достаточно
мало отличающихся соответственно от чисел
достаточно
мало отличающихся соответственно от чисел ![]() и
и
![]() ,
соответствующие значения функции
,
соответствующие значения функции ![]() ,
как угодно мало отличаются от числа
,
как угодно мало отличаются от числа ![]() .
.
Записывают: 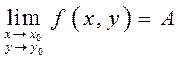
Определение.
Функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() ,
если она определена в этой точке и
,
если она определена в этой точке и 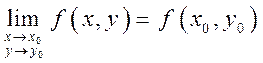 .
.
1.2 Производные и дифференциалы
Рассмотрим
функцию двух переменных ![]() .
Будем считать аргумент
.
Будем считать аргумент ![]() постоянным.
Аргументу
постоянным.
Аргументу ![]() дадим
приращение
дадим
приращение ![]() .
Тогда
.
Тогда ![]() получит
приращение:
получит
приращение: ![]() .
.
Это частное приращение ![]() по
по
![]() ,
которое обозначается:
,
которое обозначается:
![]()
4
Аналогично определяется
частное приращение ![]() по
по
![]() :
:
![]()
Определение.
Частной производной функции ![]() по
по
![]() называется
предел отношения частного приращения
называется
предел отношения частного приращения ![]() к
к
![]() при
при
![]() :
:
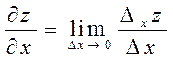
Аналогично
определяется частная производная ![]() по
по
![]() :
:
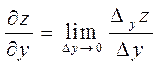
Частные производные можно обозначить и так:
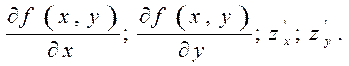
Так как частная производная является обыкновенной производной от данной функции, взятой в предположении, что изменяется только переменная, по которой производится дифференцирование, то отыскание частных производных элементарных функций осуществляется по известным правилам дифференцирования функций одной переменной.
Примеры. Найти производные функций:
а) ![]() ;
;
б) ![]()
![]() .
.
Решение: а) Найдем ![]() .
При этом
.
При этом ![]() считаем
постоянной величиной:
считаем
постоянной величиной:
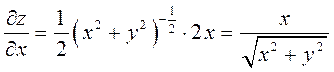
Найдем ![]() .
При этом
.
При этом ![]() считаем
постоянной величиной:
считаем
постоянной величиной:
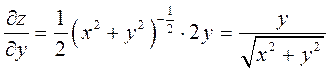
5
б) ![]() ;
При дифференцировании по
;
При дифференцировании по ![]() функция
является степенной, а при дифференцировании по
функция
является степенной, а при дифференцировании по ![]() -
показательной. Находим:
-
показательной. Находим:
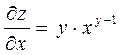 ;
;
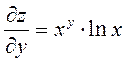 .
.
Определение.
Частным дифференциалом по ![]() функции
функции
![]() называется
главная часть частного приращения функции
называется
главная часть частного приращения функции ![]() :
:
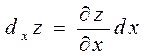
Аналогично частный
дифференциал функции ![]() по
по
![]() :
:
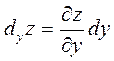
Рассмотрим
функцию ![]() и
дадим приращение аргументу
и
дадим приращение аргументу ![]() и
аргументу
и
аргументу ![]() .
Получим полное приращение функции
.
Получим полное приращение функции ![]() :
:
![]()
Определение.
Главная часть полного приращения функции ![]() называется
полным дифференциалом этой функции:
называется
полным дифференциалом этой функции:
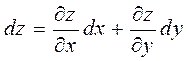
Определение.
Выражение ![]() является
полным дифференциалом, если существует такая функция
является
полным дифференциалом, если существует такая функция ![]() ,
полный дифференциал которой равен данному выражению:
,
полный дифференциал которой равен данному выражению:
![]()
Теорема: Для
того, чтобы выражение ![]() было
полным дифференциалом, необходимо и достаточно соблюдение тождества:
было
полным дифференциалом, необходимо и достаточно соблюдение тождества:
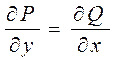
Пусть задана дифференцируемая функция:
6
![]() , при этом
, при этом ![]() ,
,
![]() .
.
Тогда ![]() ,
то есть
,
то есть ![]() -
сложная функция от
-
сложная функция от ![]() и
и
![]() .
Имеют место формулы:
.
Имеют место формулы:
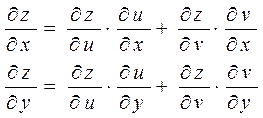
Пример. Найти ![]() ,
,
![]() функции:
функции:
![]()
Решение. Положим ![]() ;
;
![]() ,
значит
,
значит ![]() .
Получим:
.
Получим:
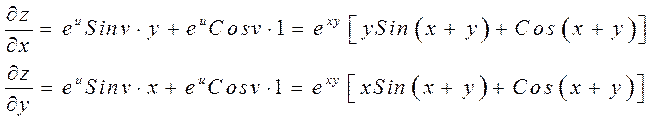
Допустим, что
функция ![]() имеет
частные производные
имеет
частные производные 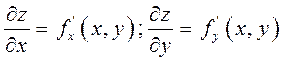 .
.
Эти производные в
свою очередь являются функциями независимых переменных ![]() и
и
![]() .
Частные производные этих функций называются частными производными второго
порядка от функции
.
Частные производные этих функций называются частными производными второго
порядка от функции ![]() и
обозначаются так:
и
обозначаются так:
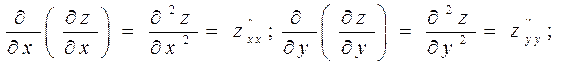
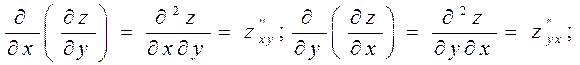
Производные ![]() ,
,
![]() называются
смешанными. Если смешанные производные непрерывны, то они равны между собой:
называются
смешанными. Если смешанные производные непрерывны, то они равны между собой:
![]()
7
Пример. Найти вторые производные функции: ![]()
Решение.
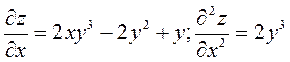
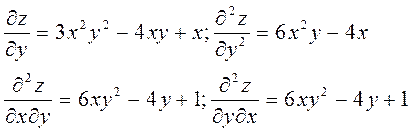
Примеры для самостоятельного решения.
1. Найти частные производные функций:
а) ![]() ;
;
б) ![]() ;
;
в) 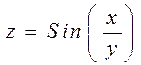 ;
;
г) 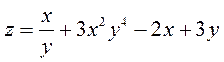 .
.
2. Найти полный дифференциал
функции: ![]() .
.
3. Найти вторые производные
функции: ![]() .
.
2.1 Объем цилиндрического тела, определение двойного интеграла
Определение.
Цилиндрическим телом называется тело, ограниченное плоскостью ![]() ,
поверхностью
,
поверхностью ![]() ,
с которой любая прямая, параллельная оси
,
с которой любая прямая, параллельная оси ![]() ,
пересекается не более, чем в одной точке, и цилиндрической поверхностью,
образующие которой параллельны оси
,
пересекается не более, чем в одной точке, и цилиндрической поверхностью,
образующие которой параллельны оси ![]() (рисунок
2.1).
(рисунок
2.1).
8
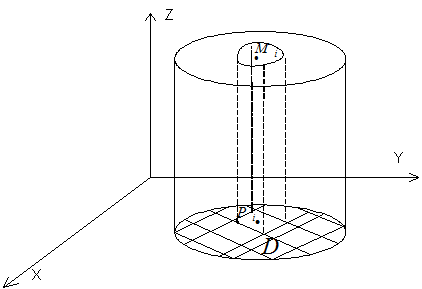
Рисунок 2.1
Основание цилиндрического тела – область ![]() в плоскости
в плоскости ![]() .
Поставим задачу: найти объем цилиндрического тела. Разобьем основание
цилиндрического тела – область
.
Поставим задачу: найти объем цилиндрического тела. Разобьем основание
цилиндрического тела – область ![]() –
на
–
на ![]() областей
произвольной формы, площади которых
областей
произвольной формы, площади которых ![]() .
Через границу каждой частичной области проведем цилиндрическую поверхность с
образующей, параллельной оси
.
Через границу каждой частичной области проведем цилиндрическую поверхность с
образующей, параллельной оси ![]() .
Цилиндрическое тело разобьется на
.
Цилиндрическое тело разобьется на ![]() частичных
цилиндрических тел. Выберем на каждой частичной области
частичных
цилиндрических тел. Выберем на каждой частичной области ![]() по
точке
по
точке ![]() и
вычислим значения функции
и
вычислим значения функции ![]() в
этих точках
в
этих точках ![]() .
Заменим частичные цилиндрические тела прямыми цилиндрами с высотами
.
Заменим частичные цилиндрические тела прямыми цилиндрами с высотами ![]() .
Тогда объем каждого частичного цилиндрического тела будет приближенно равен
объему прямого цилиндра:
.
Тогда объем каждого частичного цилиндрического тела будет приближенно равен
объему прямого цилиндра:
![]()
Объем всего цилиндрического тела:
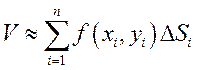
Это равенство тем
точнее, чем больше ![]() ,
тогда:
,
тогда:
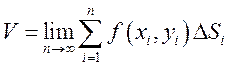
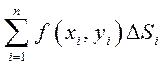 называется
называется
![]() -й
интегральной суммой для функции
-й
интегральной суммой для функции ![]() в
области
в
области ![]() .
.
9
Определение.
Предел, к которому стремится ![]() -я
интегральная сумма при
-я
интегральная сумма при ![]() называется
двойным интегралом от функции
называется
двойным интегралом от функции ![]() по
области
по
области ![]() .
.
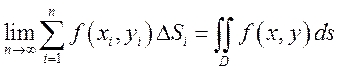
Этот предел не зависит от способа разбиения
области ![]() на
частичные области и от выбора точек
на
частичные области и от выбора точек ![]() .
В частности, если разбить область
.
В частности, если разбить область ![]() прямыми,
параллельными осям
прямыми,
параллельными осям
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.