Основные формулы. Примеры решения задач. Механические и электромагнитные колебания. Электромагнетизм

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Хабаровский институт инфокоммуникаций (филиал)

Сибирский государственный университет

телекоммуникаций и информатики

Кафедра математики и физики

Диск к практикуму по физике

для 1го курса технических специальностей

Хабаровск 2007

СОДЕРЖАНИЕ

1 Механика. 3

1.1 Основные формулы.. 3

1.2 Примеры решения задач. 5

2 Электростатика. 16

2.1 Основные формулы.. 16

2.2 Примеры решения задач. 17

3 Электрический ток. 20

3.1 Основные формулы. 20

3.2 Примеры решения задач. 20

4 Электромагнетизм.. 20

4.1 Основные формулы.. 20

4.2 Примеры решения задач. 20

5 Механические и электромагнитные колебания. 20

5.1 Основные формулы.. 20

5.1.1 Механические колебания. 20

5.1.2. Электромагнитные колебания. 20

5.2 Примеры решения задач. 20

Учебная литература. 20

1 МЕХАНИКА

1.1 Основные формулы

Скорость и ускорение материальной точки:

а) поступательное движение

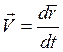      (1) 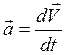                   (2), где  - радиус-вектор точки.

Для равномерного движения:

 (3);     (4);     (5).

Для равнопеременного движения:

 (6);  

 (7) – для равноускоренного движения;

  (8) – для равнозамедленного движения.

            

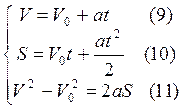
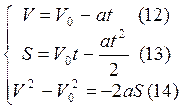
Для свободного падения без начальной скорости, V₀=0, a=g.

                      .

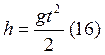
б) вращательное движение

Угловая скорость и угловое ускорение материальной точки:

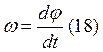
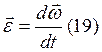           , где φ – угол поворота радиуса-вектора точки.

Для равномерного вращательного движения:

                              

Для равнопеременного движения:

               

 - для равноускоренного вращательного движения;

 - для равнозамедленного вращательного движения.

            

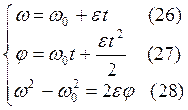
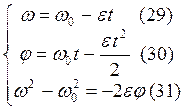
Угловая скорость ω связана с линейной скоростью:

, где  - тангенциальное (или касательное) ускорение;

 - нормальное (или центростремильное) ускорение.

                     .

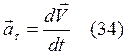
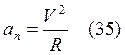Основной закон динамики поступательного движения (II закон динамики Ньютона):

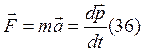, где

m – масса тела,

 - импульс тела.

Законы сохранения импульса и энергии для изолированной системы тел:

                            

 - полный импульс системы,

Е – полная энергия системы, равная сумме кинетической и потенциальной энергии тел системы.

Основной закон динамики вращательного движения абсолютно твердого тела:

, где  - вращательный момент,

J – момент инерции твердого тела,

 - угловое ускорение тела.

Момент импульса твердого тела:

.

1.2 Примеры решения задач

Пример1

Зависимость координат х, у частицы от времени t имеет вид: 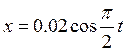, м 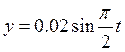, м. Определить: а) уравнение траектории у(х), б) скорость V и ускорение а в момент времени t=0.

Дано:

, м , м t = 0	Уравнение траектории можно определить, решив систему уравнений х(t), у(t) с исключением времени t
у(х) - ? V - ?, а - ?

Из (43, 44) следует:   ,   .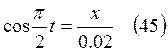

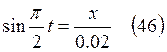Так как 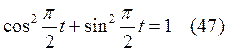, то с учетом (45, 46) 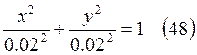 или .

Из уравнения (29) следует, что траектория имеет вид окружности радиусом 0,02 м. Определим через производные выражения скоростей V_x, V_y и ускорений а_х, а_у.

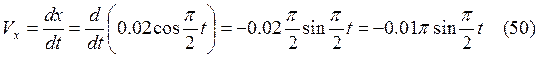
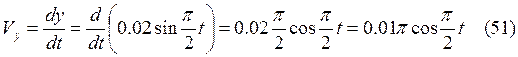
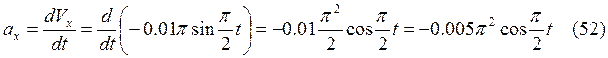
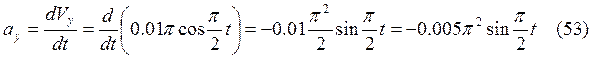
Учтем, что , .

При t = 0, V_x = 0, V_y = 0,01π

Тогда по (54) .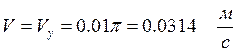

При t = 0, .

Тогда по (55)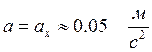

Ответ: ,    ,    .

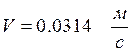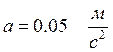Пример 2

Пароход идет по реке от А к В со скоро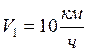стью  относительно берега, а обратно со скоростью 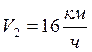. Найти: среднюю скорость парохода, скорость течения реки.

Дано

	Обозначим <V> - средняя скорость парохода,    t1 – время движения по течению реки, t2 – время движения против течения, V1 – скорость против
<V> - ? Vреки - ?

течения, V₂ – скорость по течению.

Общий путь от А к В и от В к А равен S_общ = 2S₁ (56).

                              

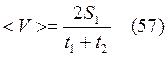
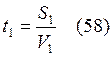
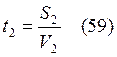
Из (57, 58, 59)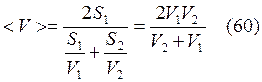

Обозначим V_р – скорость течения реки, V₀ – скорость парохода в стоячей воде.

Тогда   

Из (61, 62)  откуда .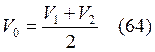

Из (61) . С учетом (64, 65)

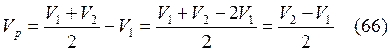
Вычисления: по (60)   

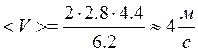
по (66)    .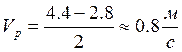

Ответ: ;  .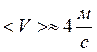

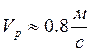Пример 3

Тело падает с высоты 1960 м без начальной скорости. Какой путь пройдет тело за последнюю секунду падения? За какое время тело пройдет последний метр пути?

Дано:

h = 1960 м V0 = 0 a = g = 9.8 м/с	Обозначим: h – вся высота падения за время t h1 – высота падения за время без последней секунды, то есть за время (t-1)

 - высота падения за последнюю секунду.

   (66).

Из (16) 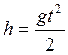; Аналогично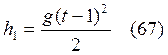

Из (66, 16, 67) .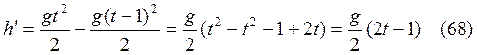

Из (16) .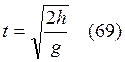

Из (68, 69) .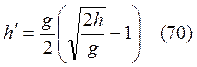

Высота падения без последнего метра равна  (71).

Обозначим t₀ – время падения с высоты h₀.

Из(16) 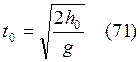. Тогда время  пройденное за последний метр пути, равно . С учетом (69, 71) получим

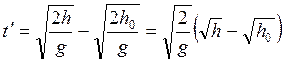     (73)

Вычисления по (70), (73).

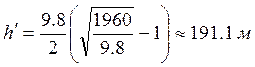
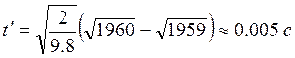
Ответ: ,   .

Пример 4

Тело брошено под углом α к горизонту. Максимальная высота подъема равна , S – дальность полета. Пренебрегая сопротивлением воздуха, определить угол α.

Дано:

hmax =
α - ?

Из рисунка:  (74)

 (75)

h_max – максимальная высота подъема

S – дальность полета

Траектория тела, брошенного под углом к горизонту, представляет собой параболу.

Движение рассматривается в плоскости XOY. Фактически тело участвует в двух движениях:

- вдоль оси «x» - равномерно и прямолинейное, то есть проекция скорости .

- вдоль оси «y» - равнопеременное, так как до точки А тело движется равнозамедленно, а после прохождения точки А равноускоренно с ускорение a=g.  - проекция начальной скорости на ось «y».

Из (13) для движения вдоль оси «y» до точки А

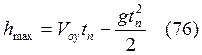, где t_n – время подъема до точки А.

Из (12) .

Так как в точке А, V_y = 0, то из (77) получим: , откуда 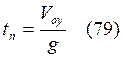. С учетом (75): .

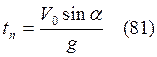С учетом равномерного движения по оси «х» , где t – общее время движения по параболе.

Так t=2t_n (83), то из (74, 80, 82) следует:

.

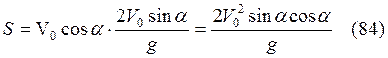По условию h_max =  (85)

Из (81, 84, 85) следует:

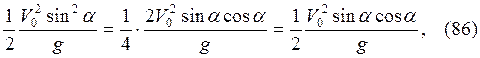
то есть sin α = cos α (87), что соответствует значению α = 45⁰.

Ответ: α = 45⁰.

Пример 5

Колесо автомашины вращается равнозамедленно, за время 2 мин угловая скорость изменилась от 240 об/мин до 60 об/мин. Определить угловое ускорение ε и число оборотов за это время.

Дано:

t = 2 мин = 120 с ω0 = 240 об/мин ≈25,12 рад/с ω = 60 об/мин ≈ 6,28 рад/с	Для равнозамедленного вращатель-ного движения используем формулы (29, 31), откуда Число оборотов
ε - ? N - ?

Вычисление по (88 – 90)

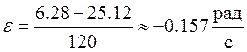
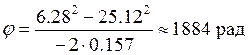
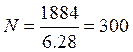
Ответ: 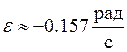, знак (-) означает характер движения, равнозамед-ленное. оборотов.

Пример 6

На рисунке показаны 3 тела, m₁ = 10 кг, m₂ = 10 кг, m₃ = 8кг. Массой блоков и трением в блоках пренебречь. Коэффициент трения тела массой m₂ равен 0,15. Определить силу натяжения нитей и ускорение тел.

Дано:

m1 = 10 кг m2 = 10 кг m3 = 8кг μ = 0,15
Т1 - ? Т2 - ? а - ?

Решение задачи на движение связанных тел основано на составлении уравнений движения для каждого из тел с учетом основного закона динамики Ньютона. На рисунке показаны силы, действующие на каждое тело:

- На тело m₁:  - сила тяжести,  - сила натяжения нити

- На тело m₂: сила тяжести  и реакция опоры  (компенсируют друг друга по III закону динамики, как силы действия и противодействия),  - сила натяжения нити,  - сила трения,  - сила натяжения нити со стороны тела массой m₃.

- На тело m₃:  - сила тяжести,  - сила натяжения нити.

Уравнение движения:

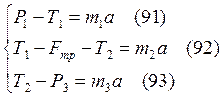
Сложим (92, 93). .

Из (91) .

Подставим (95) в (94)

Из (96)

Из (97)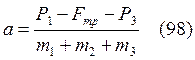

Учтем: , ,

Из (98 – 101) получим: .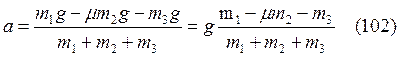

Из (91, 99)

Из (93, 101)

Вычисления АО (102, 103, 104) g ≈ 10 м/с²

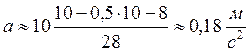
Ответ: , ,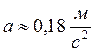

Пример 7

Пуля массой 15 г летит горизонтально и попадает в шар массой 1,5 кг, висящий на нити длиной 1м. В результате неупругого удара пуля застревает в шаре, а нить с шаром отклоняется на угол 30⁰. Определить скорость пули.

Дано:

m = 15 г = 0,015 кг М = 1,5 кг l = 1 м α = 300
Vпули - ?

Из рисунка в ΔОАВ 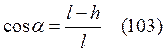, где l– длина нити, h – высота шара после удара.

Из (103)  .

Для неупругого удара пуля массой m, движущейся со скоростью V_пули и шара массой М закон сохранения импульса имеет вид:

, где U – скорость совместного движения шара с пулей.

Из (105) 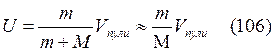 (так как по значению m<<<M).

Используем закон сохранения энергии с учетом, что после удара