Случайные события. Виды событий.
Теория вероятности изучает закономерности, возникающие в случайных экспериментах, результат которых заранее нельзя предугадать. Не все случайные эксперименты можно изучать методами теории вероятности, а лишь те которые могут быть воспроизведены в одних и тех же условиях, хотя бы мысленно какое угодно число раз. Пространством элементарных исходов называется множество содержащие все возможные взаимно исключенные результаты данного случайного эксперимента. Элементы множества называются элементарными исходами.
Событие наз-ся подмножеством данного множества. Говоря, что произошло событие А. Если эксперимент завершается одним из элементарных исходов входящих во множество А. Элементарный исход это мельчайший неделимый результат экспериментов, а событие может состоять из одного или нескольких исходов.
Событие называется случайным, если при определении определенных условий оно может произойти или не произойти. Событие называются единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием. Достоверным событием называется событие, включающее все элементарные исходы из эксперимента и которое обязательно произойдет в результате эксперимента при выполнении определенного комплекса условий.
Событие наз-ся невозможным, которое не может произойти в рез-те эксперимента при определенном комплексе условий и не содержит ни одного элементарного исхода. Событие называется равновозможными, если есть основание считать, что ни одно из них не является более возможными изменить другие. Противоположными называются события одно, из которых исключает появление другого. Пересечением событий А и В называется событие, что произошли оба сразу события А и В. Объединением событий А и В называется событие состоящее в том, что из 2х событий случилось хотя бы одно. Вероятность события А наз-ся отношение числа благоприятствующих исходов к общему числу и сходов этого события.
Свойства вероятностей.
а) вероятность достоверного события равна единице, т.к. число благоприятствующих исходов равно числу общих исходов m=n.
Р(А)=m/n=1.
б) вероятность невозможного события равно 0, т.к число благоприятствующих исходов = 0. Р(А) =m/n=0/n=0
в) вероятность случайного события 0< m/n <1 0<Р(А)<1
Равномерное распределение.
Равномерным распределением вероятности непрерывной случайной величины Х, заданной точностью вероятности на интервале (a, b)
![]()
Найдем значение С, применяя свойства плотности вероятности
![]()
Расписав данный интеграл на всей числовой оси получим
![]()
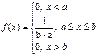
Характеристики равномерного распределения:
а) интегральная функция распределения
![]()
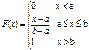
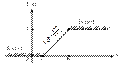
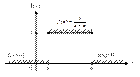
б) математическое ожидание. Применим определение мат. ожидания для непрерывной случайной величины.
![]()
![]()
Мат. ожидание равномерного распределения есть среднее арифметическое, т.е. середина интервала.
в) дисперсия. Применим определение дисперсии непрерывной случайной величины.
![]()
![]()
г) среднеквадратическое отклонение.
![]()
![]()
д) вероят. того, что случ. величина появится на интервале (α; β)
x є (a, b), найдем вероятность на интервале (α; β). P(α<x<β).
Применим формулу для вычисления вероятности на интервале для непрерывной случайной величины. P(α<x<β) = F(β) – F(α)
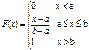
![]()
Нормальное распределение.
Нормальным распределением называют распределение вероятностей непрерывной случайной величины, заданной плотностью вероятности
![]()
σ – среднеквадратичное отклонение а – мат.ожидание х – случ. величина
Исследование:
а) область определения вся числовая ось б) если плотность вероятности f(x)>0, то график лежит выше оси Х
в) экстремумы функции
![]()
Точки перегиба х1 = а+σ х2 = а-σ
Значение функции в точках перегиба
![]()
![]()
Вывод: нормальное распределение определятся 2мя параметрами мат.ожиданием и среднеквадратичным отклонением. График нормального распределения симметричен относительно мат.ожидания
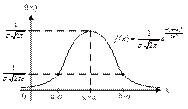
Хар-ки нормального распределения:
а) мат.ожидание
![]()
б)дисперсия
![]()
в) среднеквадратичное отклонение
![]()
г) вероятность на интервале (α; β)
![]()
д) вероятность отклон. нормально распределенной случ. величины Х по абс. величине < заданного положительного числа |x-a|<δ равно 2м интегральным функциям Лапласа от аргумента δ/σ
![]()
Плотность распред. вероятности непрерывной случ. величины.
Дифференц. функцией распред. или плотностью вероятности f(x) называется 1ая производная от интегральной функции распределения. f(x) = F’(x).
Свойства:
а)вероятность того, что непрерывная случайная величина Х примет значение из интервала (а, b) равна определенному интегралу от плотности вероятности на интервале (a, b).
![]()
б) интегральная функция распределения равна несобственному интегралу 1го рода от плотности вероятности.
![]()
в) дифференц. функция есть неотрицательная функция, то дифференц. функция тоже неотрицательная. F(x)≥0 => f(x)≥0.
г) несобственный интервал 1го рода от плотности вероятности на интервале (-∞; +∞) равна 1.
![]()
Числовые характеристики непрерывной случайной величины:
а) математическое ожидание
![]()
б) дисперсия
![]()
в) среднее квадратическое отклонение
![]()
Влияние параметров норм. распред. на форму норм. кривой.
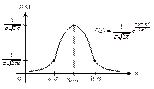
а) т.к. плотность вероятности f(x) содержит разность (х-а) в четной степени
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.