Приемники сигналов, обеспечивающие в определенном смысле минимальные искажения сообщения при приеме сигналов в условиях воздействия помех, называют оптимальными, или идеальными. В зависимости от назначения приемника критерии и количественные характеристики искажений могут быть различны.
Статистическая теория оптимального приема имеет ряд разветвлений и может рассматриваться как группа теорий с единой статистической методикой подхода к явлениям. К ним относятся: теория обнаружения сигналов (наиболее часто задача обнаружения встречается в радиолокационных системах); теория распознавания сигналов (типичная задача распознавания возникает при приеме дискретных сигналов в цифровых системах передачи); теория оценок параметров сигналов (задача оценок параметров возникает прежде всего в аналоговых импульсных системах передачи); теория фильтрации (теория оценки процессов, задача фильтрации практически возникает во всех системах при передаче и измерении непрерывных процессов, с задачей фильтрации перекликается задачей демодуляции); теория совместного обнаружения, распознавания и оценки параметров. Эти задачи наиболее часто возникают в цифровых системах передачи непрерывных и дискретных сообщений при приеме сигналов со случайно изменяющимися сопутствующими параметрами
Оптимальный приемник – приемник работающий в соответствии с критерием оптимального разбиения пространства S на SL по числу символов m.
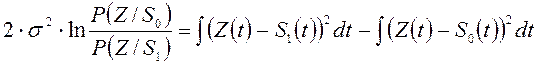 |
S1,S0 – уровни «1» и «0», σ – средне квадратичное отклонение шумов.
![]() P(Z/Sw0), P(Z/Sw1) – условные вероятности
появления «0» или «1» при наличии шумов.
P(Z/Sw0), P(Z/Sw1) – условные вероятности
появления «0» или «1» при наличии шумов.
![]()
– рассеяние мощьности смеси
сигнал- шум вокруг «1» и «0» соответственно.
Физический смысл алгоритма состоит в том, что разность из правой части показывает какой сигнал поступил в приемник (если разность больше 0 – следовательно «1», и наоборот – если меньше ноля то «0»).
![]() S1
S1
 |
 |
 |
 |
||||
![]()
![]()
![]()
![]()
![]() -- f²
∫
-- f²
∫
![]()
![]()
![]()
![]()
![]()
![]()
![]()


 Р.У.
Р.У.
-- f² ∫
S0
Рис 14. Структурная схем оптимального приемника.
Помехоустойчивость для различных видов модуляции различна и определяется вероятностью ошибки, которая зависит от соотношения сигнал/шум на входе демодулятора. Для разных видов модуляции эта зависимость различна:
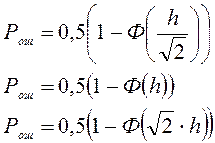
Для Амплитудной модуляции
Для Частотной Модуляции
Для Фазовой Модуляции
где Ф(z) функция Крампа, вычисляемая с помощью таблицы.
Отсюда видно, что при переходе от системы АМ к системе ЧМ энергетический выигрыш по мощности равен 2,а при переходе к системе ФМ – 4.
Когда в начале 40-ч годов в радиосвязи стали применять ЧМ, помехоустойчивость значительно возросла по сравнению с ранее используемой системой АМ. Это объясняется не увеличением потенциальной помехоустойчивости. Которая для обеих систем одинакова, а , главным образом, тем, что оптимальная решающая схема для ЧМ реализуется с довольно большой точностью, а при АМ этому препятствует невозможность обеспечить точной оптимальное значение ненулевого порогового уровня. Поэтому реальная помехоустойчивость при ЧМ близка к потенциальной, а при АМ значительно ниже ее.
Система ФМ, как и другие системы с противоположными сигналами, обеспечивает максимальную для двоичной системы потенциальную помехоустойчивость. однако реализация демодулятора для когерентного приема ФМ встречает определенные трудности. При построении демодулятора с активным фильтром возникает проблема поддержания равенства фаз опорного генератора и приходящего сигнала.
Энергетический выигрыш при переходе от ДАМ к ДЧМ И ДФМ.
Рис 15.ДАМ в векторной форме.
U1
![]()
![]()
![]()
![]() Ес=(U1-U0)²=а²
Ес=(U1-U0)²=а²
а а длинна вектора U0U1
U0
Рис 16.ДЧМ в векторной форме.
![]() U1
U1
![]() a²
a²
a² U0
Рис 17.ДФМ в векторной форме.
![]() U1
U1
![]() Ec=2
a²
Ec=2
a²
U0
Таким образом, из приведенных выше диаграмм видно, что наибольшую энергетику дает ДФМ, а наименьшую ДАМ.
Вероятность ошибки в идеальном приемнике:
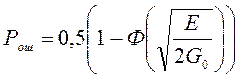
Алгоритм Котельникова для частотной модуляции:
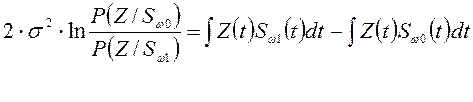 |
 |
 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()



 Х ≈
Х ≈
«1»
Гоп Р.У.
«0»
Х ≈
 |
Гоп
Рис 18.Схема, реализующая алгоритм Котельникова для Частотной модуляции.
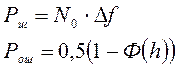
∆f=1/T опт; ∆f=2/T неопт
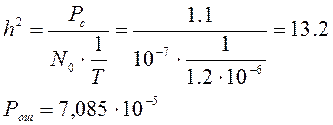 |
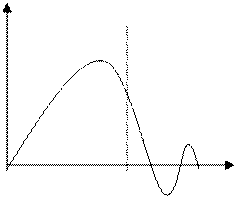
Где а, t0 – постоянные. Функция g(t) оказывается зеркальным отражением s(t) относительно оси, проведенной через точку t0/2. Для физической реализуемости фильтра необходимо и достаточно, чтобы g(τ)=0 при τ<0.
Реакция согласованного фильтра на финитный сигнал s(t) длительностью Т существует лишь на финитном интервале протяженностью 2Т.
Согласованный фильтр хорошо пропускает те частоты, которые дают больший вклад в энергию сигнала.
 |
 |
||
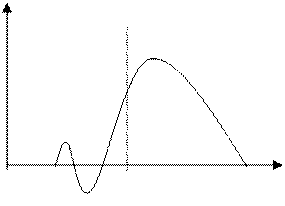
Рис 19. Сигнал и импульсная реакция согласованного фильтра.
Следует отметить, что задачей согласованного фильтра является не восстановление формы сигнала, искаженной шумом, а получение одного отсчета, по которому можно судить о присутствии или отсутствии на входе фильтра сигнала известной формы.
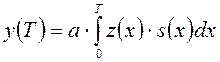 |
Таким образом, в момент времени Т напряжение на выходе согласованного фильтра пропорционально сигналу на входе интегратора
Можно сказать, что выбранная схема приемника когерентного ЧМ приемника
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.