Разработка системы связи. Сравнение выбранной схемы приемника с оптимальной. Передача аналоговых сигналов методом ИКМ

Одной  из  схем  реализации  оптимального  некогерентного  приема является  схема,  которая  основана  на  применении  согласованных фильтров (рисунок 2.2.1).

Пусть приемник содержит согласованные фильтры для двух вариантов ожидаемого сигнала - 1 и 0. Принятый сигнал x(t) поступает на входы обоих фильтров. Напряжения на выходе фильтров подаются на  детекторы (Д),  которые  выпрямляют  напряжение  на  выходах  согласованных фильтров,   т.е.   выделяют  огибающую   (модуль)   функции  взаимной корреляции 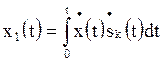.  В каждом из каналов берутся отчеты величины огибающей через определенный момент времени t (накопление этих значений огибающей происходит в интеграторе). Через время t происходит их сравнение в решающем устройстве. Полярность выходного напряжения зависит от того, какое из сравниваемых напряжений больше.

Большое  распространение  имеют  схемы  с  неоптимальным  методом некогерентного приема. В таких схемах вместо согласованных фильтров используются «разделительные» фильтры,  имеющие относительно узкие полосы  пропускания,  т.е.  настроенные  на  определенные  частоты. Преимуществом таких схем является в одних случаях простота, в других случаях  -  менее  жесткие  требования  к  стабильности  частоты.  Но, несмотря   на   относительную   простоту   этих    схем,    теория помехоустойчивости  для  них  оказывается  сложной  и  полностью  не разработанной.

2.3 Расчет вероятности ошибки на выходе приемника.

Для нахождения вероятности ошибки на выходе приемника необходимо знать  тип  модуляции  (в  данном  случае  частотная),  вид  приёма (некогерентный),  мощность  полезного  сигнала  на  входе  приёмника (Рс = 0.6 Вт (В²)), полосу пропускания согласованных фильтров (f = 5Fc, где Fc - ширина спектра сигнала).

Найдем вероятность ошибки при передаче аналоговых сигналов методом импульсно-кодовой модуляции (ИКМ). Для этого первоначально вычислим мощность помехи (шума) на выходе приемника по формуле:

 ,                                                                                                            (2.3.1)

где N₀ – помеха - белый шум.

,  .

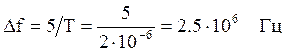Отсюда:

.

Найдем отношение мощности полезного сигнала на входе приемника к мощности шума на выходе приемника - h²:

    .                                                                                                      

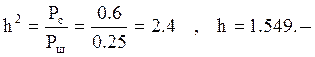Для расчёта вероятности ошибки на выходе приёмника воспользуемся формулой:

.                                                                                                       (2.3.2)

.

Мы получили слишком большую вероятность ошибки, оставлять такой ее нельзя. Исправить это можно, увеличив значение мощности сигнала на входе приемника. Пусть у нас  Тогда

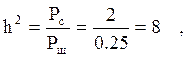 и

.

Это значение Р_ош приемлемо для нашей системы связи.

2.4 Сравнение выбранной схемы приемника с оптимальной.

Задача оптимального приема была решена в 1946 году академиком В. А. Котельниковым. В случае приема двоичной информации алгоритм действия такого идеального приемника имеет следующий вид:

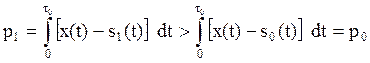                                                    (2.4.1)

Данный алгоритм справедлив, когда априорные вероятности символов одинаковы,. Таким образом, решающая схема должна выбрать тот, из ожидаемых сигналов, который имеет наименьшее среднеквадратическое отклонение от принятого сигнала. Для сигналов, энергии которых одинаковы,     т.е. 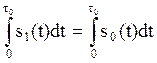 , неравенство (2.4.1) переписывается в виде:

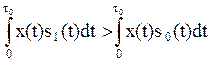                                                                                 (2.4.2)

Структурная схема приемника, реализующего алгоритм (2.4.1) приведена на рисунке 2.4.1.

Принимаемый сигнал x(t), который представляет собой смесь сигнала с помехой , поступает на вычитающие устройства, к каждому из которых подводится генератор опорного сигнала  или , представляющего точную копию передаваемого x(t). Напряжения с вычитающих устройств возводятся в квадрат в соответствующих нелинейных цепях с квадратичной характеристикой и интегрируются    путем    заряда    через    большие    сопротивления конденсаторов.  В момент  напряжения с конденсаторов поступают на   решающую схему, устроенную так, чтобы выдавать на выходе номер конденсатора, имеющего наименьшее напряжение. Очевидно, что в результате этих операций определяется тот символ, который удовлетворяет   неравенству   (2.4.1).   После   этого   конденсаторы разряжаются путем мгновенного закорачивания, и схема оказывается готовой к приему следующего элемента сигнала. Это справедливо в том случае, когда сигналы равновероятны. В том случае, когда это не так, конденсаторы следует заряжать до напряжения,  численно равного . При этом нетрудно убедиться, что схема будет работать в соответствии с правилом:

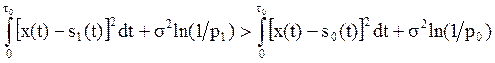                             (2.4.3)

Рассмотренная схема не пригодна для применения на практике