коммутационный блок координатной станции типа АТСК поступает простейший поток вызовов, который создает нагрузку Уб эрланг при средней длительности занятия входа блока tБ. Блок обслуживается одним маркером, работающем в режиме с условными потерями при постоянной длительности занятия tМ. Задержанные вызовы обслуживаются в случайном порядке, независимо от очередности их поступления.
Определить вероятность ожидания свыше допустимого времени tД и среднее время ожидания задержанных вызовов tЗ. Значения Уб = 45 эрл , tБ=90 с , tМ=0.8 с и tД = 3.2 с
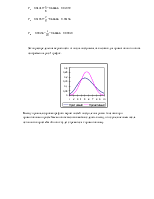
С помощью формул Берка построены кривые (рис.1 и рис.2 приложения 3 данного УМД). Эти кривые дают возможность определить требуемые значения: вероятность ожидания свыше времени t, т.е. P (γ > t) и среднее время ожидания
tЗ = tм · γ в зависимости от нагрузки на маркер.
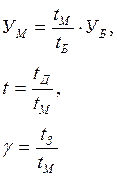
УМ, t, γ - Время измеренное в единицах длительности занятия.
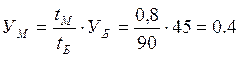Эрл
Определяем по найденному значению УМ с помощью кривой рис.2 приложения 3
γЗ = f ( УМ )
γЗ = 0.88
Определим среднее время ожидания задержанных вызовов:
tЗ = tм · γ= 0,8 · 0.88 = 0.704
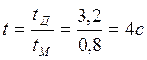
По графику на рис.1 приложения 3 определим вероятность ожидания свыше допустимого времени tД = 3.2 с:
P (γ > t'Д) = f(УM , t) =0.006
Неполнодоступный пучок линий однозвенной системы с отказами обслуживает нагрузку У эрланг при доступности d.
Определить емкости пучка V при двух значениях потерь Р1 и Р2. Сравнить полученные результаты. Величины У=25 эрл, d=15, Р1 =1‰ и Р2=3‰
Воспользуемся методом О’Делла. В данном методе емкость пучка определяется как
, но при фиксированных значениях d и P формула приобретает вид линейной зависимости числа соединительных
устройств от интенсивности нагрузки:
, где a и b определяются по приложению 4 УМД.
1) Для P1=1‰ и d=15 получаем a=1.58 и b=5.4. С помощью этих коэффициентов можно определить V1:
=1.58·25+5.4= 45
Для дальнейших расчетов принимаем емкость пучка равной:
V=V1=45
Предварительное запараллеливание нужно проводить так, чтобы получить число групп:
q=(2÷4)
=(2÷4)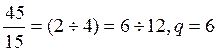
При g=6 имеется больше возможностей запараллеливания.
С точки зрения экономии выбираем:
q=6; V=45
 |
Решаем систему:
V-d = 30= 5·k1+2· k2 + k3
Рассчитаем структурные параметры:
k1 =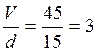 
30 = 5 *3+2 k2+k3
k2=7; k3=1
k6=45-18-21- 2=4
k6= 4
2) Рассчитаем структурные параметры равномерной неполнодоступной схемы цилиндров при значении Р2:
Для P2=3‰ и d=15 получаем a=1.47 и b=4,9. С помощью этих коэффициентов можно определить V2:
=1.47·25+4,9=42
Для дальнейших расчетов принимаем емкость пучка равной:
V=V2=42
Предварительное запараллеливание нужно проводить так, чтобы получить число групп:
q=(2÷4) =(2÷4)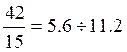
При заданных V и d необходимо определить точки коммутации, принадлежащие разным группам и различным шагам искания путем запараллеливания по r и r+1, где r определяется по формуле:
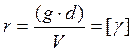
Для определения соответствующих точек коммутации необходимо
определить число линий 
, полученных
путем запараллеливания по (r+1) точку и число линий 
, полученных путем
запараллеливания по r точек. Эти значения определяются по
следующим соотношениям:
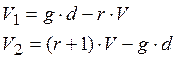
Для определения этих значений удобнее если коэффициент уплотнения представить в целой и дробной части, в которой не производится сокращение:
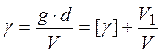
Выбираем g=6, V=42
Определим и :
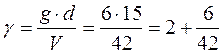
- для r=2
Рассчитаем число шаговых цилиндров:
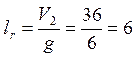
Проверим правильность схем:
По рассчитанным параметрам построим матрицу связности и неполнодоступную схему рис. 5.1 и рис. 5.2
1)
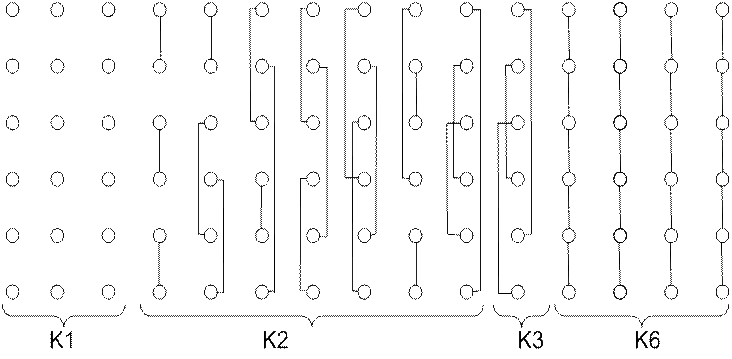
Рисунок 5.1
Матрица связности будет выглядеть следующим образом:
2)
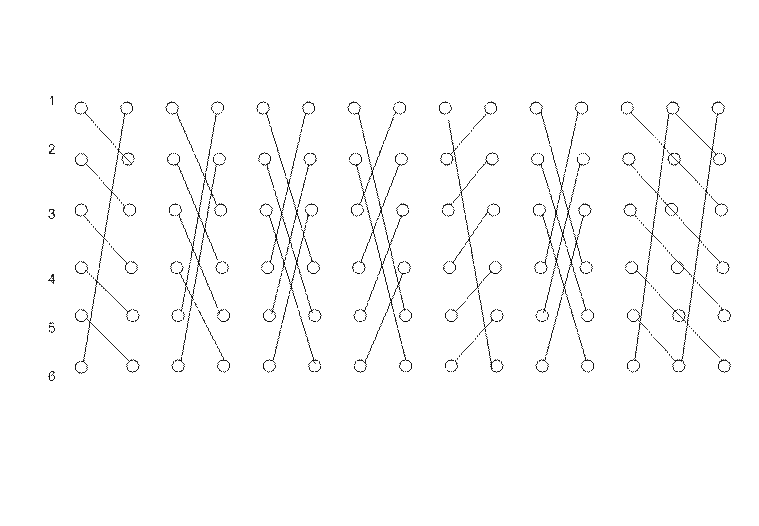
Рисунок 5.2 – Неполнодоступная схема включения со сдвигом
Неполнодоступная система построена правильно, так как разница между двумя элементами столбца не превышает по абсолютной величине 1.
В неполнодоступной схеме со ступенчатым включением число соединений между точками коммутации отдельных нагрузочных групп больше, чем в равномерной неполнодоступной схеме цилиндров. Из расчетов видно, что при увеличении потерь емкость пучка как схемы со ступенчатым включением, так схемы цилиндров, уменьшается и это приводит к более эффективному использованию соединительных линий.
Нагрузка, поступающая на ступень ГИ АТСК, обслуживается в данном направлении пучком линий с доступностью KBq . При потерях Р=0.005. Нагрузка на один вход ступени а, нагрузка в направлении У.
Определить методом эффективной доступности емкости пучка V, при установке на ступени блоков 60 x 80 x 400 и 80 x 120 x 400. Сравнить полученные результаты.
Величины KBq=20 , У=35
θ=0.7
a=0.45
Воспользуемся методом эффективной доступности
1. Рассчитаем емкость пучка для блока 80 x 120 x 400со структурными параметрами:
na=13.33
ma=kB=20
f=1
Для расчета воспользуемся формулой:
Коэффициенты α и β найдем из приложения 4 УМД. Необходимо знать значения вероятности потерь и эффективной доступности пучка.
Эффективная доступность пучка вычисляется по формуле:
где
q -
коэффициент, определяемый зависимостью потерь от доступности и распределением
вероятностей доступности. В данной задаче необходимо принять q = 0.7. Математическое
ожидание доступности :
где
Ym-интенсивность нагрузки, обслуженной m промежуточными линиями.
Интенсивность нагрузки определяется как:
Yma=a·na=0.45 · 13.33 = 5.9 эрл
Найдем число выходов:
g =
Определим значение доступности dэ по выше предложенным формулам:
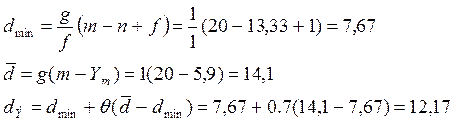
По
известным значениям Р=5‰ и dэ=20 с помощью Приложения 4 УМД найдем число линий(емкость пучка): 
2. Аналогично определим емкость пучка для блока 60 x 80 x 400 со структурными параметрами:
na=15
ma=kB=20
f=1
По ранее использовавшимся формулам рассчитаем интенсивность нагрузки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.