3.3.1 Расчет фильтра для выделения третьей гармоники.
Рассчитаем
фильтр для выделения третьей гармоники. Т.к частота колебаний, генерируемых
автогенератором 14,8кГц, то для третьей гармоники будет 44,4 кГц. Обозначу f0 = 44,4 кГц. Найду теперь граничные частоты
полосового фильтра. Зная 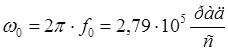 , и задавшись f3 =
50 кГц, а значит и
, и задавшись f3 =
50 кГц, а значит и 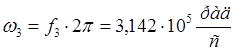 , нетрудно найти
, нетрудно найти ![]() :
:
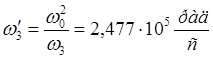
Учитывая
соотношение (3.1), также известную связь 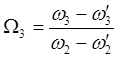 определим
определим
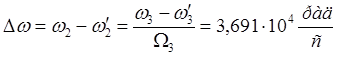 .
.
Решая систему

получаем:
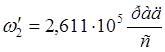
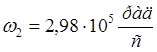
Таким образом, граничные частоты получились равными:
![]() кГц
кГц
![]() кГц
кГц
![]() кГц
кГц
![]() кГц
кГц
Пользуясь справочной таблицей, находим полюсы передаточной функции фильтра-прототипа:
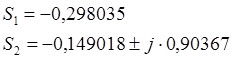
Для отыскания полюсов передаточной функции полосового фильтра воспользуемся соотношением:
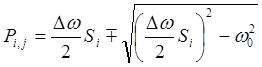 ,
,
Полученные значения полюсов удобно представить в виде таблицы 2.3:
Таблица 2.3 Значения полюсов передаточной функции
|
Номер полюса |
Полюсы H(p) полосового фильтра |
|
|
|
|
|
|
1,2 |
0,55 |
27,896 |
|
3,5 |
0,259 |
26,28 |
|
4,6 |
0,291 |
29,61 |
Передаточная функция полосового фильтра может быть записана в виде произведения трех сомножителей второго порядка:
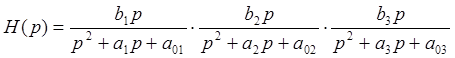
Найду коэффициенты передаточной функции:
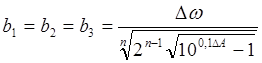
Подставив
значения, получим ![]() . Коэффициенты при p в знаменателях сомножителей
. Коэффициенты при p в знаменателях сомножителей ![]() , а свободные члены
, а свободные члены ![]() , где
, где ![]() и
и ![]() - действительная и
мнимая части i-того полюса передаточной функции.
- действительная и
мнимая части i-того полюса передаточной функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.