




АЛГОРИТМЫ И СТРУКТУРНЫЕ СХЕМЫ ЦФ
Цифровой фильтр - это вычислительное устройство (физическая система или программа для ПЭВМ), реализующее заданный алгоритм избирательной обработки сигналов в реальном масштабе времени. Другими словами, цифровой фильтр - это дискретная система, которая преобразует последовательность x(k) отсчётов входного сигнала в последовательность y(k) отсчётов выходного сигнала.
Линейный цифровой фильтр, работающий во временной области, в общем виде описывается линейным разностным уравнением N-го порядка
M−1 N−1
y(k∆t) + ∑bm у(k∆t − m∆t) = ∑anx(k∆t − n∆t), k = 0, 1, 2,…, M ≥ N ,где m =1 n = 0
N, М, аn, bm - постоянные фильтра; k - номер отсчёта входной последовательности (сигнала) х(k∆t); ∆t = 1/fд и fд - шаг и частота дискретизации аналогового сигнала.
Максимально допустимый шаг ∆tmax, соответственно минимальную частоту fд.min дискретизации входного сигнала x(t) выбирают на основе теоремы отсчётов (теоремы Котельникова) [4, с. 257]:
∆tmax = 1/2fm; fд.min = 1/∆tmax = 2 fm,где fm - максимальная частота спектра сигнала x(t), определяемая на основе, например, энергетического критерия [4, с. 243].
Для уменьшения влияния перекрытия соседних спектров, обусловленных дискретизацией аналогового сигнала x(t), минимальную частоту дискретизации fд.min увеличивают в 3…5 раз, т. е fд = (6…10)fm.
Для преобразования и обработки сигналов и изображений используют различные частоты дискретизации. Так, в системах связи fд = 8 кГц, в звукотехнике fд = 40…48 кГц, в системах обработки ТВ-изображений fд = 14 МГц. В современном цифровом оборудовании телецентров приняты следующие стандарты на частоту дискретизации: для обработки сигналов fд = 48 кГц; для передачи сигналов по каналу связи fд = 32 кГц; для лазерного проигрывателя fд = 44,1 кГц.
С целью упрощения расчётов и возможности сопоставления частотных характеристик различных фильтров принимают шаг дискретизации ∆t = 1/ f€д = 1. Тогда нормированная частота дискретизации f€д = 1 Гц, а частоту сигнала (или частоты его спектральных составляющих и помех) выражают в долях от частоты f€д, т. е. f€= (0…0,5) f€д; приэтом нормированная (цифровая) частота w = f€/ f€д = 0…0,5. Зная ненормированную частоту дискретизации fд, нетрудно восстановить реальную шкалу частот, используя выражение f = w fд.
В общем случае выходной сигнал y(k) (при ∆t = 1) в текущий момент времени k∆t определяется значением входного сигнала х(k) в тот же момент времени k, значениями входного и выходного сигналов в предшествующие моменты времени k - n (n > 0) и описывается разностным уравнением вида y(k) = a0x(k) + a1x(k −1) + a2 x(k − 2) + ... + aN−1x[(k − (N −1)] − (1)
− b1y(k −1) − b2 y(k − 2) −... − bM −1y[(k − (M −1)], M ≥ N, где x(k - n) и y(k - m) - задержанные соответственно на n и m отсчётов входной и выходной сигналы.
Все реальные сигналы являются каузальными (причинными). При их математическом описании удобно совмещать начало отсчёта аргумента k = 0 с началом сигнала и считать, что он равен нулю при значении аргумента k, меньшем нуля, т. е. x(−k) = 0.Соответственно y(−k) = 0, т. к. на выходе устойчивого фильтра не может
появиться сигнал, опережающий первый отсчёт x(0) входного сигнала.
Соотношение между выходным и входным сигналами в ЦФ обычно представляют в z-области в виде системной (передаточной) функции ЦФ N∑−1ak z−k
![]() H(z)
=
YX((zz)) =
1+k =M∑0-1bmz−m =
H(z)
=
YX((zz)) =
1+k =M∑0-1bmz−m =
m=1
![]() =
a10++b1az1z−1−1++b2az2−z2−2+ +... ... + +bMaN−1−z1z−(−M(N−−1)1) , (2)
=
a10++b1az1z−1−1++b2az2−z2−2+ +... ... + +bMaN−1−z1z−(−M(N−−1)1) , (2)
где z = ep∆t; N - 1 ≥ 0; М - 1 ≥ 1.
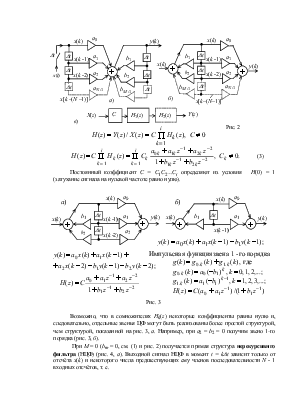
Общее описание ЦФ уравнениями (1) и (2) позволяет создать набор алгоритмов, которые непосредственно используют для реализации ЦФ в виде специального устройства (на базе специализированных микропроцессоров типа DSP-5600x, DSP-5630x, TSP-320xх и др.) или в виде программ для ПЭВМ [6]. Этот набор алгоритмов создаётся путём варьирования величин N, М, аn и bm.
Для реализации какой-либо заранее выбранной функции типа (1) или (2) можно подобрать множество цифровых фильтров, составленных на основе трёх элементов [4, c.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.