Алгоритмы и структурные схемы ЦФ. Вычислительное устройство (физическая система или программа для ПЭВМ), страница 3

Принципиальное различие между нерекурсивными и рекурсивными фильтрами заключается в свойствах их импульсных характеристик. В первом случае импульсная характеристика содержит конечное число отсчётов, не превышающем N, а во втором,

a)                                              б)                           ^a

∆t

x(t)

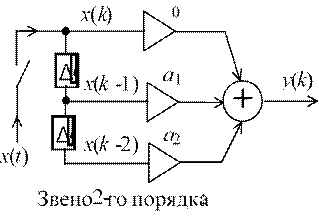
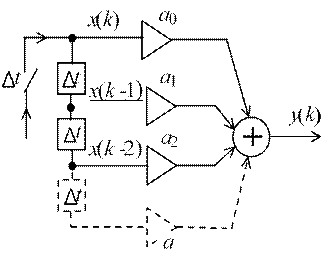
y(k) = a₀х(k) + a₁х(k - 1) + a₂х(k - 2);

        x[k –(N –1)]     ^{N -1}     g(k) = {a₀ , a₁, a₂};   H(z) = C (a₀ + a₁z^-1 + a₂z^-2)

Рис. 4

благодаря обратной связи, число отсчётов теоретически бесконечно велико. В связи с этим нерекурсивные фильтры часто называют КИХ-фильтрами (фильтры с конечной импульсной характеристикой), а рекурсивные - БИХ-фильтрами (фильтры с бесконечной импульсной характеристикой).

При этом структура и коэффициенты системной функции H(z) НЦФ однозначно связаны с коэффициентами импульсной функции g(k) фильтра, а в РЦФ эти связи выражены неявным образом. Отсчёты импульсной функции g(k) РЦФ, имеющей вид неогра-ниченно-протяжённой          последовательности, можно определить (используя свойства линейности и задержки z-преобразования) посредством суммирования соответствующих отсчётов импульсных функций звеньев 2-го порядка. 

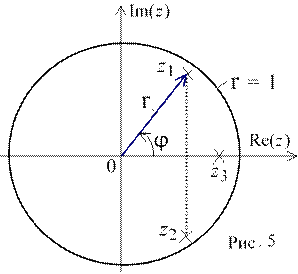
Если полином знаменателя системной функции H(z) имеет вещественные коэффициенты, то его корни (полюсы) лежат либо на вещественной оси zплоскости (например, полюс z3), либо образуют комплексно-сопряжённые пары (например, полюсы z1 и z2, рис. 5). 

При определении нулей и полюсов в z-плоскости целесообразно преобразовать функцию H(z) к виду без отрицательных степепей z, т. е.

H(z) = a10++ba11zz−1−1++ba22zz−2−2 = a0zz22++b1az1z++b2a2 .

Откуда комплексно-сопряжённая пара полюсов

 z₁,₂ =−b₁ / 2 ± j b₂ − b₁² / 4 = re^{± jϕ}= r cosϕ± jrsinϕ.

Приравняв вещественные и мнимые части

               − b₁ / 2 = r cosϕ;       b₂ − b₁² / 4 = b₂ − r² cos² ϕ= rsinϕ,получим:

k) = g0(k)

где  g(rg0обратные=((k)b=2 a; 0ϕr ^kсоотношени=−+arccos(g_sin1(_ϕk) +b1яg/:2  2b(r)k)==, −−2arccos(r cosϕb1и/ 2b2b=2 r)2=).−sinarctg(kϕ)4,bk2=/1b,122,3−,...;1

                                            sin(k +1)ϕ, k =1 0,1,2,...; g1(k) = a1rk −1    sinϕ

Тогда импульсная функция звена 2-го порядка РЦФ 

При  а0 = 1 и а1 = а2 = 0 системная функция

H(z) =1/(1+ b₁z⁻¹ + b₂ z⁻² ) = z² / z² + b₁z + b₂ , а его реакция на единич-

  gg(k2)(k=)r=_kasin2r^ksin(k⁻²+_ϕ^sin1)ϕsin⁽,^kk⁻_ϕ=¹⁾0^ϕ,1,, 2k,=...2, 3, 4,....

ный импульс ^δ(k)при нулевых начальных условиях

Выражение импульсной функции звена 1-го порядка РЦФ приведено на рис. 3, б.

Если системная функция РЦФ представлена в виде выражения (2), то импульсную функцию g(k) (см. (7)) фильтра записывают, пользуясь следующим мнемоническим правилом:

-  коэффициенты а_n при ^δ(k ⁻ n) равны коэффициентам числителя  функции H(z)

при z^-k, k = 0, 1, 2,…, N - 1;

-  коэффициенты b_m при g(k ⁻ m) равны коэффициентам знаменателя (с обратным знаком) функции H(z) при z^-k , k = 1, 2,…, М - 1.

                     Например, для звена                   2-го порядка РЦФ с системной функцией

H(z) = (a₀ + a₁z⁻¹ + a₂z⁻² ) /(1+ b₁z⁻¹ + b₂ z⁻² ) импульсная функция g(k) = a₀δ(k) + a₁δ(k −1) + a₂δ(k − 2) − b1g(k −1) − b2g(k − 2).

Для трёхзвенного РЦФ с системной функцией 

H(z) = a1+b11z −2 . a 1 +b22 z z2−2 . a1+b13z 1 +b23z 2−2 = 1 +b21z 2 1+b12 z

А

_{= 0} +А1z−1⁻1++BА22zz−⁻22++BА33zz−3⁻3++BА44zz−⁻44++BА55zz−⁻55++BА66zz−⁻66 _,

1+B1z ^где A0 ⁼ a01a02a03; A1 ⁼ a01a02a13 ⁺ a01a12a03 ⁺ a11a02a03;

A2 ⁼ a01a02a23 ⁺a01a12a13 ⁺a11a02a13 ⁺a01a22a03 ⁺a11a12a03 ⁺a21a02a03; A3 ⁼ a01a12a23 ⁺a11a02a23 ⁺a01a22a13 ⁺a11a12a13 ⁺a21a02a13 ⁺a11a22a03 ⁺

⁺a21a12a03; A4 ⁼ a01a22a23 ⁺a11a12a23 ⁺a21a02a23 ⁺a11a22a13 ⁺a21a12a13 ⁺     

⁺a21a22a03; A5 ⁼ a11a22a23 ⁺a21a12a23 ⁺a21a22a13; A6 ⁼ a21a22a23; B1 ⁼ b13⁺b12 ⁺b11; B2 ⁼ b23 ⁺b12b13 ⁺b11b13 ⁺b22 ⁺b11b12 ⁺b21;

B3 ⁼ b12b23 ⁺ b11b23 ⁺ b22b13 ⁺ b11b12b13 ⁺ b21b13 ⁺ b11b22 ⁺ b21b12;

B4 ⁼b22b23⁺b11b12b23⁺b21b23⁺b11b22b13⁺b21b12b13⁺b21b22;

               B5⁼b11b22b23⁺b21b12b23⁺b21b22b13; B6 ⁼b21b22b23^,           

расчёт отсчётов импульсной функции можно вести, пользуясь выражением g(k) = А₀δ(k) + А₁δ(k −1) + А₂δ(k − 2) + ... + А₆δ(k − 6) − −В1g(k −1) −В2 g(k − 2) − ... −В6g(k − 6).