Алгоритмы и структурные схемы ЦФ. Вычислительное устройство (физическая система или программа для ПЭВМ), страница 2

268]: сумматора (условное обозначение на схемах ⊕), умножителя (> ) и элемента задержки ( ^∆t ), соотношения между входом x(k) и выходом s(k) которых: N−1

                   s_⊕(k) = ∑anx(k − n);      s_>(k) = anx(k);     s_∆t (k) = x(k −1).    

n=0

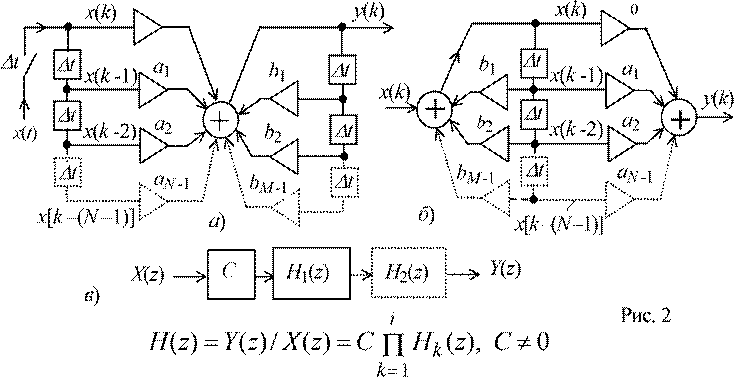
На рис. 2, а   представлена прямая структура рекурсивного фильтра (РЦФ), согласно которой для расчёта выходного сигнала у(k) (см. выражение (1)) используются по меньшей мере одно значение входного сигнала х(k) и одно из полученных ранее значений выходного сигнала  у(k - m),     m = 1, 2,… (т. е. у РЦФ не все  коэффициенты bm равны нулю). Эта структура содержит один сумматор, умножители и N + M - 2 элементов задержки (для создания цепей, соответствующих числителю и знаменателю системной функции (2), используют отдельные элементы задержки).

Кроме прямых структур часто используют прямую каноническую, каскадную (последовательную) каноническую, параллельную каноническую и комбинации четырёх структур. Под канонической реализацией подразумевают форму, при которой число элементов задержки ∆t равно порядку системной функции (т. е. равно наивысшей степени полинома знаменателя (числителя) системной функции H(z), рис. 2, б). В данной работе будет использована прямая каскадная каноническая форма реализации ЦФ, имеющая минимальное число элементов задержки и состоящая из i биквадратных звеньев (рис. 3, а). В этой структуре выходная последовательность предшествующего звена фильтра является входной для последующего звена, а эквивалентная системная функция H(z) равна произведению системных функций H_k(z) отдельных биквадратных звеньев (см. рис. 2, в): 

a0                                                                                                                                                      a

H(z) =С kП=1Hk (z) = kП=1Ck  01k++b1ak1zk−z1−1++b2ak2zk−z2−2 , Ck ≠ 0.            (3) i        i           а

Постоянный коэффициент С = С1С2…С_i определяют из условия   H(0) = 1  (затухание сигнала на нулевой частоте равно нулю).

x(k)                                     a                                                               a

+y(ak2)x=(ka0−x2(k))−+b1ay1(xk(k−−1)1)−+b2−y2(k −  2Импульсная);                                                                                gg(0k.k) (₌kфункция)g=_0.a_k0(k(−)bзвена₊1)gkk₁−_.,1_kk,(¹kk=^-)=,0го1,_где,1порядка,22,,...;3,...;

H(z) =Ca1+b1z 1 +b2z 2 Hg1(.kz()k=)C=(aa10(−+b1a)1z−1)/(1+b1z−1)

Рис. 3

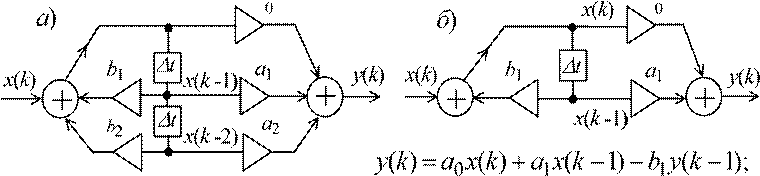
Возможно, что в сомножителях H_k(z) некоторые коэффициенты равны нулю и, следовательно, отдельные звенья ЦФ могут быть реализованы более простой структурой, чем структурой, показанной на рис. 3, а. Например, при а2 = b2 = 0 получим звено 1-го порядка (рис. 3, б).

При M = 0 (bm = 0, см. (1) и рис. 2) получается прямая структура нерекурсивнго фильтра (НЦФ) (рис. 4, a). Выходной сигнал НЦФ в момент t = k∆t зависит только от отсчёта x(k) и некоторого числа предшествующих ему членов последовательности N - 1 входных отсчётов, т. е.

y(k) = a0x(k) + a1x(k −1) + a2x(k − 2) + ...+ aN−1x[(k − (N −1)].      (4)

Например, в случае пяти ненулевых коэффициентов а_n с одинаковыми значениями имеем  пятиточечную сглаживающую функцию 

y(k) =[x(k − 2) + x(k −1) + x(k) + x(k +1) + x(k + 2)]/5, а если взять коэффициенты an - 2 =  an +  2 = - 3, an - 1 =  an + 1 = 12 и an = 17, то получим формулу сглаживания по методу наименьших квадратов  y(k) =[−3x(k − 2) +12x(k −1) +17x(k) +12x(k +1) − 3x(k + 2)]/35.

Системная функция:  прямой структуры НЦФ (см. рис. 4, а)

                H X(z)                          k = 0        a0 + a1z−1 + a2z−2 + ... + aN−1z−(N−1);  (5) каскадной структуры  НЦФ (звеньев 2-го порядка, см. рис. 4, б)

H(z) = C Пi H_k (z)= С Пi (a_0k + a₁k z−1 + a2k z−2 ).   k=1       k=1

Чтобы получить импульсную функцию g(k) ЦФ, нужно на его вход подать

единичный импульс ^δ(k), т. е.  положить x(k) =^δ(k). Тогда импульсные функции g(k) НЦФ и РЦФ соответственно равны (см. (4) и (1)):

g(k) = a₀δ(k) + a₁δ(k −1) + a₂δ(k − 2) + ...+ aN−₁δ[(k − (N −1)]; (6)

 (7)

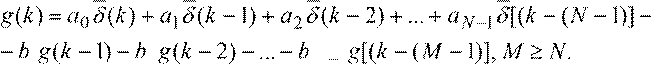                       1                      2                                M 1