ПРИМЕР РАСЧЁТА НЕРЕКУРСИВНОГО ЦИФРОВОГО
ФИЛЬТРА НИЖНИХ ЧАСТОТ
Проектируется НЦФ нижних частот с полосой пропускания wп от 0 до 0,1 (частота нормирована) и полосой задерживания wз от 0,4 до 0,5.
Допуски на отклонение АЧХ от номинального уровня: в полосе пропускания αmax = 0,1 дБ; в полосе задерживания αmin = 40 дБ.
Найти минимальное число N (порядок фильтра), позволяющее удовлетворить заданным требованиям.
Решение. 1. Запустить программу DNF.ехе. Затем щелчком левой клавиши мыши (в дальнейшем щёлкнуть мышью) на кнопке "New" главного меню (см. рис. 9, вверху слева) вызвать подменю "Параметры ЦФ". В соответствующие окна занести (с клавиатуры) исходные параметры (рис. 9, а). В окно "Порядок фильтра" занести любое нечетное число (вплоть до 999 и более), например, 17. Щелкнуть мышью на кнопках "Прямоугольное весовое окно" и "Запомнить".
2. Щелкнуть на кнопке "ЛАЧХ" главного меню, вызвав тем самым на экран дисплея график коэффициента затухания α = f(w) (рис. 9, б). Ввести (с клавиатуры) в окно "Частота 1" (внизу графика, см. рис. 9, б) значение wп = 0,1 и нажать кнопку "Enter". При этом рядом с окном будет выведено значение коэффициента затухания на границе полосы пропускания α = - 0,196 дБ (αmax = - 0,1 дБ).
3. Ввести в окно "Частота 2" значение wз = 0,4 и нажать кнопку "Enter". Рядом с этим окном выводится значение коэффициента затухания на границе полосы задерживания α = -32,996 дБ (αmin = - 40 дБ).
4. Замечаем, что для выполнения требований к АЧХ нужно увеличить порядок фильтра. Вводим N = 29 (см. рис. 9, а), щелкаем на кнопках "Запомнить" и "ЛАЧХ". График α = f(w) (рис. 8, б) автоматически обновляется, как и значения коэффициентов затухания НЦФ 29-го порядка, которые близки к заданным исходным значениям этих коэффициентов.
5. Вводим значение N = 31 (рис. 9, в) и щелкаем на кнопках "Запомнить" и "ЛАЧХ". Убеждаемся (см. рис. 9, г), что требования к АЧХ выполнены.
6. Щёлкаем на кнопках "Весовое окно Хемминга" (рис. 9, д), "Запомнить" и "ЛАЧХ". Из сравнения графиков α= f(w) (см. рис. 9, е и рис. 9, г) следует, что перехόдная полоса расширилась, "размылись" границы полос пропускания и задерживания (что означает потерю разрешающей способности фильтра) при одновременном уменьшении пульсаций АЧХ (ослаблено явление Гиббса) в полосе пропускания и лучшему их подавлению в полосе задерживания. На рис. 9, ж показан вид графика и коэффициенты "окна" Хемминга (кнопка "ВО").
2
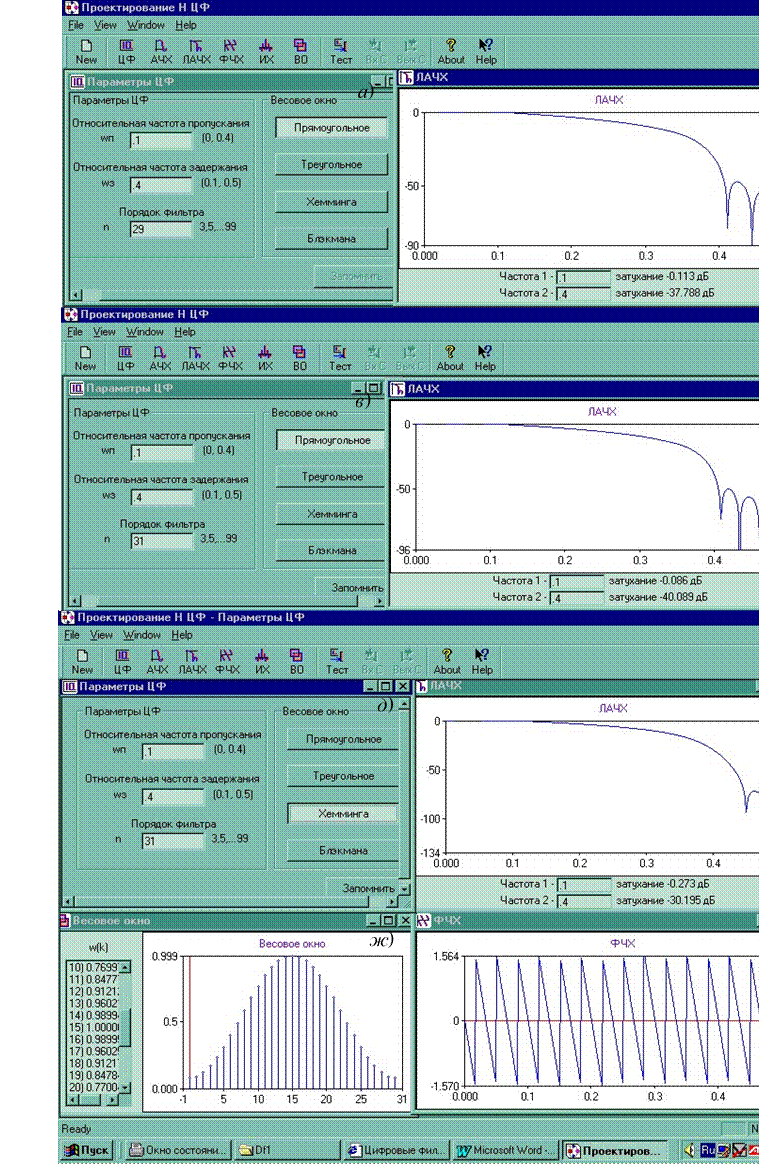Рис. 9
2
3
7. Обратите внимание на линейность ФЧХ (рис. 9, з) (кнопка "ФЧХ") и периодические скачки на π радиан.
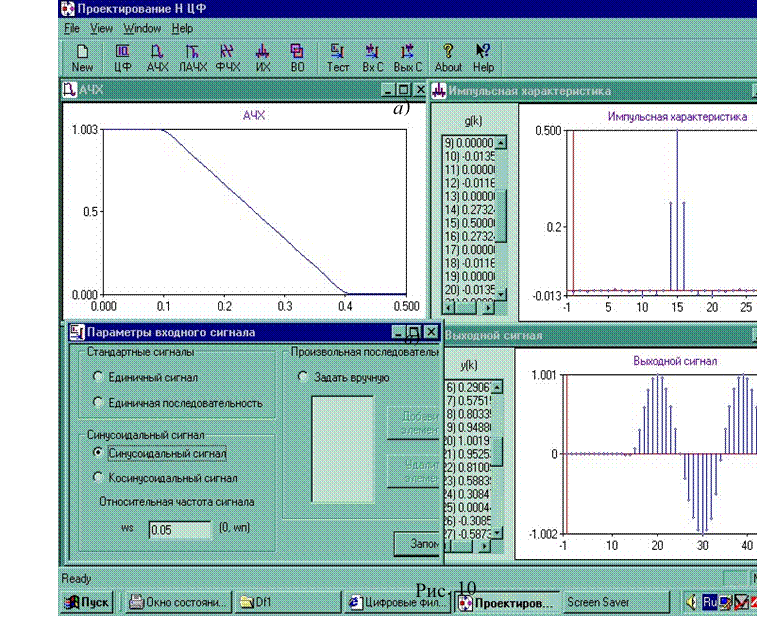
8. Величины коэффициентов ak НЦФ выводятся слева от графика его импульсной характеристики g(k) (рис. 10, б) после щелчка на кнопке "ИХ" главного меню. Проверка НЦФ на устойчивость не проводится, т. к нерекурсивные фильтры принципиально устойчивые.
9. Провести испытание синтезированного нерекурсивного фильтра. С этой целью на вход фильтра нужно последовательно подать единичный отсчёт, единичную последовательность, дискретизированный синусоидальный или косинусоидальный сигнал (количество отсчётов за период равно 1/w, где 1 - нормированная частота дискретизации; w - нормированная частота синусоидальной или косинусоидальной функции), полигармонический сигнал, произвольно набранную с клавиатуры цифровую последовательность, и проанализировать выходные последовательности.
После щелчка на кнопке "Тест" в появившемся подменю (рис. 10, в) выбрать тип и параметры соответствующего входного сигнала. В качестве примера, на рис. 10, г представлен вид выходного сигнала (кнопка "ВыхС") при подаче на вход фильтра дискретизированного синусоидального сигнала с относительной частотой w = 0,05. Соответствующий входной сигнал выводится на экран дисплея после щелчка на кнопке "ВхС".
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
