Алгоритм вычисления коэффициентов. Компонентные уравнения для индуктивных и емкостных элементов

(3.10)

Или в виде системы линейных уравнений:

(3.11)

Количество уравнений равно числу резисторов в схеме.

3.4 Алгоритм вычисления коэффициентов  и  уравнения состояния

По матрице главных сечений для произвольной схемы (2.6) запишем топологические уравнения для напряжений индуктивных хорд  и токов емкостных ребер :

	(3.12)
	(3.13)

Компонентные уравнения для индуктивных и емкостных элементов:

;

(3.14)

Заменим в (3.12) и (3.13) левые части равенства выражениями (3.14), далее выразим  через , используя (3.6) и объединим полученные уравнения в одно матричное выражение:

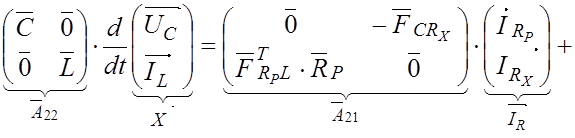
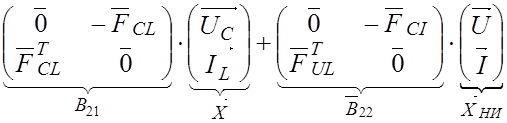
С учетом введенных обозначений:

(3.15)

Отсюда, подставив вместо  выражение (3.1) и решив уравнение относительно 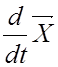, получим выражения, на которых строится алгоритм вычисления коэффициентов  и  уравнения состояния:

	(3.16)
;	(3.17)

Пример 3.2. Построить уравнение состояния для схемы (рисунок 2.1).

Определим значения матриц, через которые выражаются коэффициенты уравнения состояния в (3.15):

;

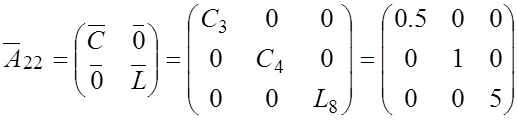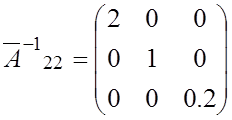
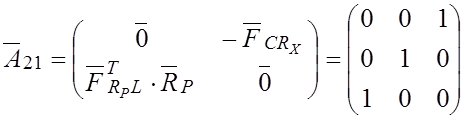
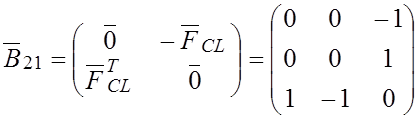
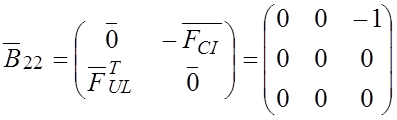
Находим коэффициенты уравнения состояния, используя вычисленные в примере 3.1 значения коэффициентов  и  уравнения токов резисторов:

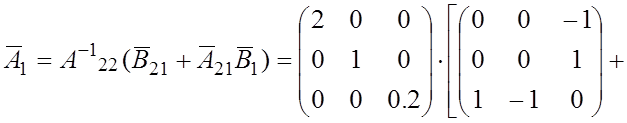
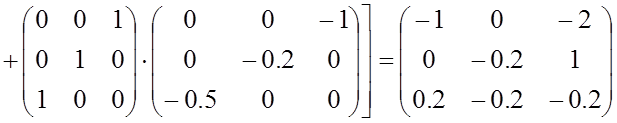
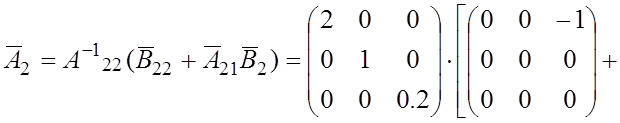
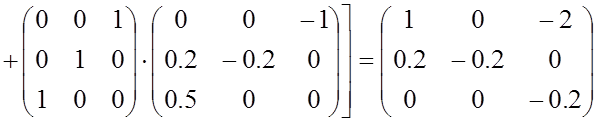
Таким образом, уравнение состояния рассматриваемой схемы

(3.18)

Или в виде системы дифференциальных уравнений

(3.19)

Количество уравнений в системе (3.19) равно числу реактивных элементов в схеме.

Решив систему (3.19) одним из известных численных методов (метод Эйлера, Эйлера-Коши и т.д.), находим значение вектора состояния 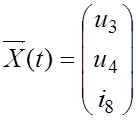, а подставив найденное решение в (3.11), находим значение токов резисторов схемы .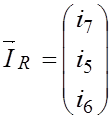

3.5 Алгоритм вычисления коэффициентов  и  уравнения выхода

Как отмечалось ранее, отклик  на выходе схемы может быть напряжением  либо током . Если отклик есть напряжение на каком-либо резистивном элементе, то его можно записать по закону Ома через ток этого элемента и его сопротивление. Например, для схемы на рисунке 2.1,  можно представить как .

Выражение для  найдем из (3.10):

(последняя строка уравнения 3.10). Окончательно получим:

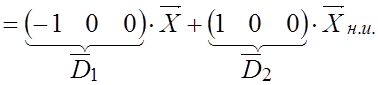
Откуда имеем:

;

Если  - есть напряжение на емкостном элементе или ток в индуктивности, т.е. принадлежит вектору состояния , то коэффициент , а  равен -й строке единичной матрицы , где -номер элемента в векторе .

Например, , тогда

;  (т.к. ).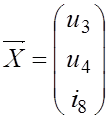

Если , то ;

Если , то .

Таким образом, для схемы на рисунке 2.1 коэффициенты уравнений математической модели имеют вид:

Коэффициенты уравнения токов резисторов:

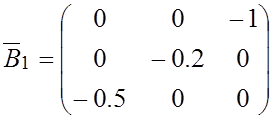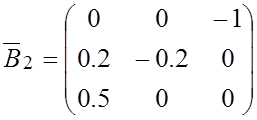, , коэффициенты уравнения состояния:

, ;

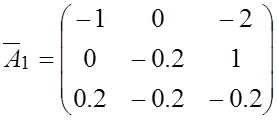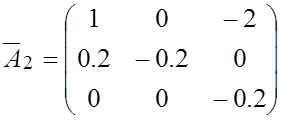коэффициенты уравнения выхода (принимаемое в качестве отклика цепи напряжение ):

;

4 Расчет характеристик линейной цепи

4.1 Характеристики линейной цепи

При анализе линейных схем часто вместо расчета токов и напряжений во всех элементах требуется находить лишь отклик цепи на заданное воздействие. В этом случае требуется знать характеристики цепи.

Характеристики линейной цепи определяются как её отклики на некоторые сигналы специальной формы. Эти сигналы выбираются таким образом, чтобы зная отклик на них, можно было предсказать (рассчитать) отклик цепи на произвольное воздействие.

В качестве таких сигналов выбирают обычно сигналы вида (рисунок 4.1, 4.2, 4.3).

Рисунок 4.1 – Гармонический сигнал
Рисунок 4.2 – Единичная функция (функция Хевисайда)
Рисунок 4.3 – Единичный импульс (функция Дирака)

Для нахождения характеристик в схеме выделяются точки, называемые входом и выходом. Ко входу подключаются независимый источник входного сигнала  специального вида (другие источники в схеме отсутствуют) и находится отклик  (рисунок 4.4), являющийся характеристикой цепи.

Рисунок 4.4

Рассмотрим характеристики цепи.

Передаточная функция. Если представить входной сигнал  и отклик  их изображениями по Лапласу соответственно  и , то их отношение является характеристикой цепи, называемой передаточной функцией.

(4.1)

Очевидно, что при , .

Переходная характеристика есть отклик цепи  на единичный скачок () при нулевых начальных условиях.

Импульсная характеристика представляет собой отклик цепи  на единичный импульс ().

Комплексный коэффициент передачи. Представим  и   векторами в комплексной плоскости, обозначив их  и , тогда их отношение: