|
|
(4.2) |
есть комплексный коэффициент передачи на частоте ![]() .
.
В формуле (4.2) ![]() -зависимость
модуля комплексного коэффициента передачи от частоты, называется амплитудно-частотной
характеристикой (АЧХ), а
-зависимость
модуля комплексного коэффициента передачи от частоты, называется амплитудно-частотной
характеристикой (АЧХ), а ![]() -зависимость от
частоты фазового угла комплексного коэффициента передачи, называется фазочастотной
характеристикой (ФЧХ) цепи.
-зависимость от
частоты фазового угла комплексного коэффициента передачи, называется фазочастотной
характеристикой (ФЧХ) цепи.
Любая из приведенных выше характеристик, полностью отражает свойства цепи. Следовательно, любая характеристика может быть получена из другой с помощью преобразований.
Зависимость между характеристиками определяется следующими соотношениями:
|
|
(4.3) |
т.е. комплексный коэффициент передачи может быть получен из
передаточной функции путем замены оператора ![]() на
на ![]() .
.
Частотная и импульсная характеристики связаны между собой парой преобразований Фурье:
|
|
-прямое преобразование Фурье; |
|
|
-обратное преобразование Фурье. |
Наконец, импульсная и переходная характеристики связаны друг с другом соотношениями:
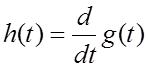 ;
;
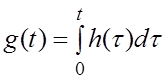
4.2 Расчет передаточной функции
В общем случае выражение передаточной функции имеет форму
дроби, числитель и знаменатель которой являются полиномами, зависящими от
оператора ![]() (
(![]() - комплексная
частота).
- комплексная
частота).
|
|
(4.4) |
Степень ![]() полинома знаменателя
полинома знаменателя ![]() равна
порядку анализируемой цепи, т.е. числу реактивных элементов в ней. В числителе
ряд коэффициентов при старших степенях
равна
порядку анализируемой цепи, т.е. числу реактивных элементов в ней. В числителе
ряд коэффициентов при старших степенях ![]() могут быть равны
нулю и степень полинома
могут быть равны
нулю и степень полинома ![]() может
быть меньше степени
может
быть меньше степени ![]() .
.
Расчет передаточной функции согласно выражению (4.4)
сводится к расчету коэффициентов полинома числителя ![]() и знаменателя
и знаменателя ![]() . Для этого
воспользуемся уравнениями состояния и выхода анализируемой цепи:
. Для этого
воспользуемся уравнениями состояния и выхода анализируемой цепи:
|
|
(4.5) |
|
|
(4.6) |
Отличия данных выражений от ранее приводимых (3.2) и (3.3)
состоит лишь в том, что вместо вектора ![]() здесь используется
скалярная величина
здесь используется
скалярная величина ![]() .
.
Представим входящие в уравнение переменные их изображениями по Лапласу. Тогда получим:
|
|
(4.7) |
|
|
(4.8) |
Решим выражения (4.7) относительно ![]() . Группируя члены,
содержащие
. Группируя члены,
содержащие ![]() , имеем:
, имеем:
![]() , откуда:
, откуда:
![]()
Подставим это выражение в (4.8):
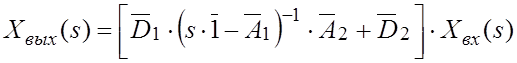 , откуда:
, откуда:
|
|
(4.9) |
Данное выражение может быть использовано для построения
алгоритма вычисления передаточной функции ![]() . Основная трудность
вычисления этого выражения состоит в нахождении обратной матрицы
. Основная трудность
вычисления этого выражения состоит в нахождении обратной матрицы ![]() . Рассмотрим метод
вычисления такой матрицы, называемой методом Леверрье-Фадеева.
. Рассмотрим метод
вычисления такой матрицы, называемой методом Леверрье-Фадеева.
Дана квадратная матрица ![]() (этим условиям
удовлетворяет матрица
(этим условиям
удовлетворяет матрица ![]() уравнения
состояния реальной схемы)
уравнения
состояния реальной схемы) ![]() -го
порядка. Все полученные в ходе вычислений матрицы будут также квадратными
матрицами
-го
порядка. Все полученные в ходе вычислений матрицы будут также квадратными
матрицами ![]() -го порядка. Примем
-го порядка. Примем ![]() и
и ![]() , проводим
вычисления по следующей схеме:
, проводим
вычисления по следующей схеме:
|
|
(4.10) |
Последнее выражение – тождество, которое можно использовать для проверки безошибочности проведенных вычислений.
В схеме вычислений в выражениях для ![]() использована
операция нахождения следа матрицы, обозначенная символом
использована
операция нахождения следа матрицы, обозначенная символом ![]() (сумма элементов
главной диагонали).
(сумма элементов
главной диагонали).
Через величины, значения которых рассчитываются в схеме Леверрье-Фаддеева можно найти характеристический полином анализируемой цепи:
![]()
и
значение обратной матрицы ![]() ,
входящей в выражение (4.5) передаточной функции
,
входящей в выражение (4.5) передаточной функции ![]() :
:
|
|
(4.11) |
Пример 4.1. Рассчитаем передаточную функцию цепи, приведенной на рисунке 2.1.
Возьмём матрицу ![]() из
уравнения состояния для данной схемы:
из
уравнения состояния для данной схемы:
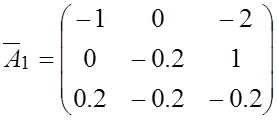 ,
,
![]()
и выполним действия в соответствие с алгоритмом вычислений (3.10):
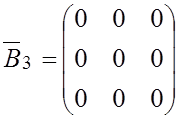 ;
; ![]() ;
;  ;
;
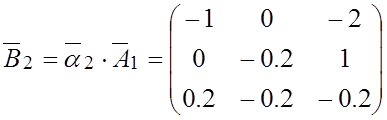 ;
; 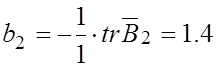 ;
;
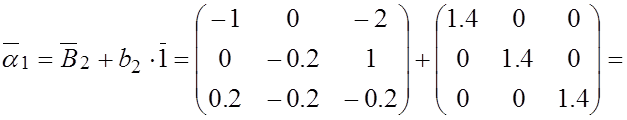
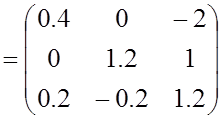 ;
;
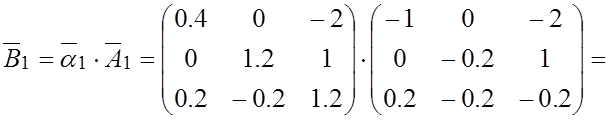
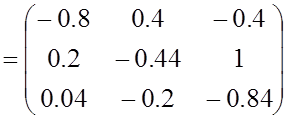 ;
; 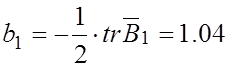 ;
;
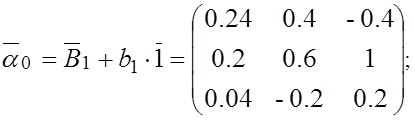
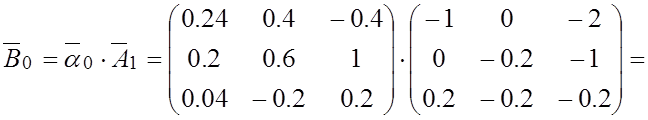
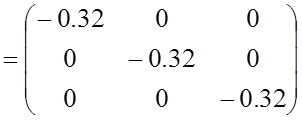 ;
; 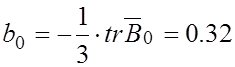 ;
;
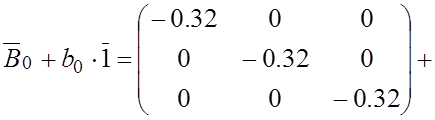
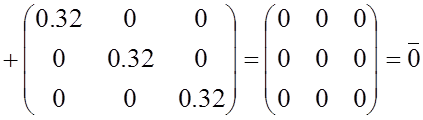
Равенство (4.10) выполняется. Это подтверждает правильность сделанных вычислений.
Пользуясь результатами вычислений находим необходимую для вычисления передаточной функции величину:
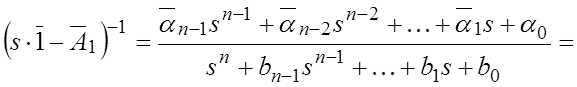
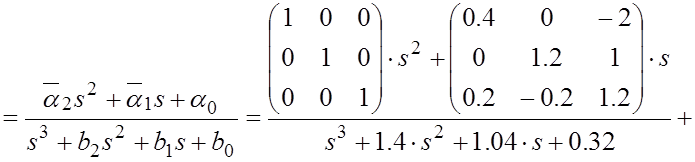
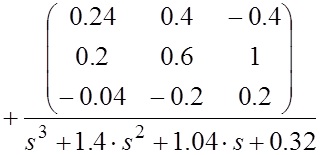
Положим, что входным источником является источник ![]() , источники
, источники ![]() и
и ![]() из схемы исключаем.
Это приводит к исключению из матрицы
из схемы исключаем.
Это приводит к исключению из матрицы ![]() соответствующих
им столбцов, т.е. в матрице
соответствующих
им столбцов, т.е. в матрице ![]() останется
только первый столбец:
останется
только первый столбец:
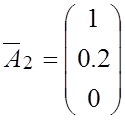
Значения коэффициентов ![]() и
и ![]() получим из уравнения
выхода. В качестве
получим из уравнения
выхода. В качестве ![]() возьмем
напряжение на резисторе
возьмем
напряжение на резисторе ![]() ,
т.е.
,
т.е. ![]() . Так как
. Так как
![]() , то
коэффициент
, то
коэффициент ![]() будет скаляром
(значения
будет скаляром
(значения ![]() и
и ![]() ) были найдены
ранее, при формировании уравнения выхода). Итак:
) были найдены
ранее, при формировании уравнения выхода). Итак:
![]() ;
;
![]()
Подставив найденные значения в (4.9), окончательно получим:
![]()
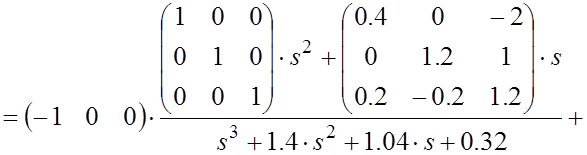
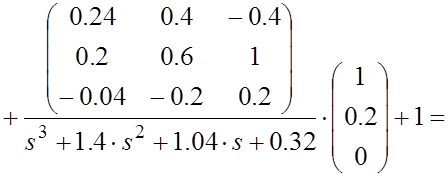
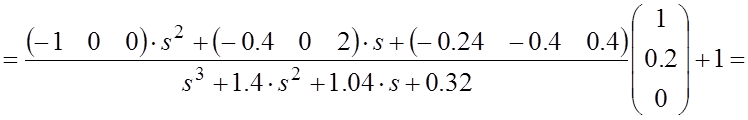
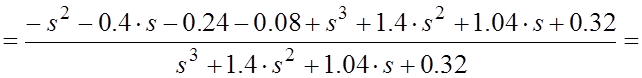
|
|
(4.12) |
Сравнивая полученные значения ![]() с выражением (4.4)
делаем вывод, что коэффициенты передаточной функции
с выражением (4.4)
делаем вывод, что коэффициенты передаточной функции ![]() равны
соответственно:
равны
соответственно:
|
|
|
|
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.