Методы анализа работы узлов аппаратуры связи. Вычисление реакции цепи с помощью интеграла Дюамеля. Определение комплексной передаточной функции цепи

Дискретизация входного сигнала и импульсной характеристики цепи.

Сигнал на выходе дискретизатора – это последовательность дискретных отсчетов U₁(n) входного сигнала u₁(t), формулы для которого получены при выполнении раздела 2 (интеграл Дюамеля). Отсчеты входного сигнала рассматриваются для моментов времени t=0, T, 2T, ….., где Т – интервал дискретизации(период дискретизации).

Согласно теореме Котельникова интервал дискретизации рассматривается из соотношения

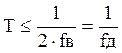
,где fв – граничная частота спектра U₁(w);

fд – частота дискретизации.

Выберем частоту, после которой значения амплитуд не превышают уровня 0.1 от максимальной амплитуды:

f_в=2500Гц, f_д=5кГц, Т=1/5000Гц=0,2мс

Далее составляется аналитическое выражение для :

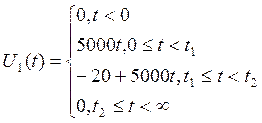
Для вычисления дискретных отсчётов входного сигнала U₁(n) в следующую формулу вместо t подставляются последовательности моментов дискретизации.

Т.к. , то дискретные отсчёты переходной характеристики рассчитываются по формуле:

Результаты вычисления дискретных отсчётов входного сигнала и переходной характеристики приведены в Таблице 5.1

Таблица 5.1 – Дискретные отсчёты входного сигнала и переходной характеристики:

t, мс	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6
N	0	1	2	3	4	5	6	7	8
U1(n), B	0	1	2	3	4	5	6	7	8
H(n)	0.4	0.268	0.18	0.12	0.084	0.054	0.036	0.024	0.016

Продолжение таблицы 5.1 - Дискретные отсчёты входного сигнала и переходной характеристики:

t, мс	1.8	2	2.2	2.4	2.6	2.8	3	3.2	3.4
N	9	10	11	12	13	14	15	16	17
U1(n), B	9	0	-9	-8	-7	-6	-5	-4	-3
H(n)	0.011	0.073	0.0049	0.0033	0.0022	0.0015	0.00099	0.00066	0.00045

t, мс	3.6	3.8	4
N	18	19	20
U1(n), B	-2	-1	0
H(n)	0.0003	0.0002	0.00013

6 Расчёт дискретных значений сигнала на выходе цепи.

Дискретные значения сигнала на выходе цепи для его первых 20 отсчётов можно найти, используя выражение дискретной свёртки:

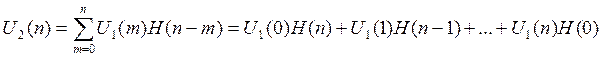
Здесь - отсчёты входного сигнала ,

 - отсчёты импульсной характеристики цепи .

Рассчитаем дискретную последовательность сигнала на выходе цифрового фильтра, соответствующего цепи, изображённой на рисунке 1.4:

…………………………………………..

Результаты вычисления дискретной последовательности сигнала на выходе цепи приведены в Таблице 6.1 .

Таблица 6.1 – Значения дискретной последовательности выходного сигнала

Продолжение таблицы 6.1 – Значения дискретной последовательности выходного сигнала

t, мс	3.4	3.6	3.8	4
N	17	18	19	20
U2(n), B	-2.8023	-2.001	-1.0812	-0.0123

7 Расчёт спектральных характеристик дискретизированного сигнала.

Спектральная плотность дискретного непериодического сигнала U₁(n) может быть найдена по формуле преобразования Фурье:

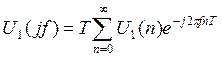, таким образом, получим:

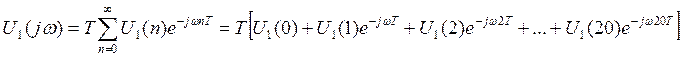            (7.1)

Результаты вычислений спектральной плотности дискретизированного сигнала U₁(n) по формуле (7.1) приведены в Таблице 7.1.

Таблица 7.1 – Значения спектральной плотности дискретизированного сигнала U₁(n)

Сравнение результатов расчёта с результатами, полученными в пункте 4 (таблица 4.1), показывает, что различие в значениях |U₁(jf)| незначительное.

График спектральной плотности дискретизированного сигнала U₁(n) представлен на рисунке 7.1

.       

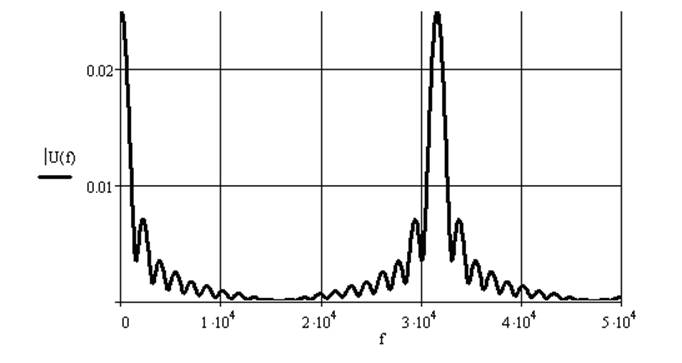
Рисунок 7.1 – График  спектральной плотности дискретизированного сигнала

8 Синтез линейных цифровых фильтров.

В основе простейшего метода синтеза цифровых фильтров лежит предположение о том, что синтезируемый фильтр должен обладать импульсной характеристикой, которая является результатом дискретизации импульсной характеристики соответствующего аналогового фильтра-прототипа:

                                                (8.1)

В общем случае синтез структуры цифрового фильтра осуществляется путём применения Z-преобразования к последовательности вида (8.1)

Находится системная функция цифрового фильтра

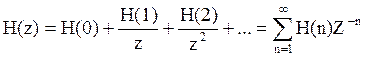
Найденную системную функцию H(z) следует сравнить с её общим выражением:

 

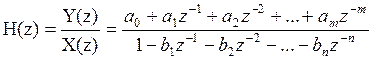
и определить коэффициенты трансверсальной (a₀, a₁, …, a_m ) и рекурсивной (b₁, b₂, …, b_n)частей H(z).

Степень приближения АЧХ синтезированного цифрового фильтра и характеристика аналогового прототипа зависит от выбранного шага дискретизации Т.

Ниже рассмотрен синтез цифрового фильтра, подобного аналоговой цепи, имеющей импульсную характеристику , найденную в разделе 1 (формула (1.2).

Получено:

Найдём отсчёт функции импульсной характеристики:

Выполнив  Z-преобразование отсчётов импульсной характеристики, получим системную функцию цифрового фильтра:

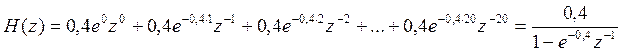
Учитывая, что Z-преобразования входного и выходного дискретных