Иерархия памяти современных компьютеров. Классификация ЗУ. Кэш-память. Программируемые логические интегральные схемы. Программируемые логические матрицы, страница 9

 – число выходов матрицы М2;

 – число конъюнкций (р-термов), необходимых для решения поставленной задачи.

Матричная схема представляет собой сетку ортогональных проводников в местах пересечения которых могут быть установлены полупроводниковые элементы с односторонней проводимостью – диоды или транзисторы (рисунок 5.3).

Способ включения полупроводниковых диодов или транзисторов в местах пересечения шин матрицы М1 позволяет реализовать на любом из ее выходов любую конъюнкцию ее входных переменных, взятых с инверсией или без знака инверсии. Способ включения биполярных или МОП транзисто-

	Рисунок 5.3-Схемотехника PLM и элементы связей в матрице И (М1) и в матрице ИЛИ (М2)

 

ров в местах пересечения шин матрицы М2 позволяет реализовать любую дизъюнкцию на любом из выходов.

5.2 Подготовка задачи к решению на основе PLM

При наличии PLM минимальной конфигурации (ограниченное число входов, выходов, промежуточных конъюнкций) следует уменьшить по возможности число термов в заданной системе функций. Минимализацию по числу переменных и термов следует вести до уровня, когда число термов становится равным q, а число переменных равным s, выбранной PLM. Если же размерность, имеющихся в наличии PLM, обеспечивает решение задачи в

	Рисунок 5.4-Карты Карно (а) для воспроизведения системы из двух функций  и  в PLM (б)

 

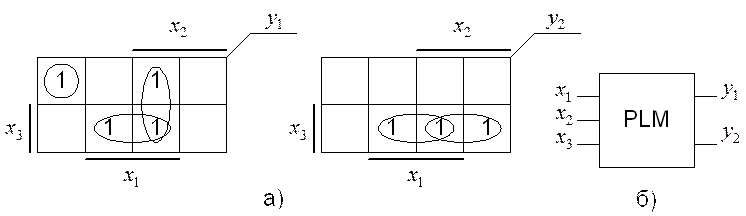
ее исходной форме, то минимализация не требуется вообще, т.к. не ведет к сокращению оборудования.

Рассмотрим пример реализации КЦС на базе PLM (рисунок 5.4)

После минимизации функции  и  принимают значения

Способ включения полупроводниковых диодов или МДП транзисторов в местах пересечения шин матрицы И (рисунок 5.5) позволяет реализовать конъюнкции:

,

,

,

.

Способ включения биполярных или МДП-транзисторов в матрице ИЛИ позволяет реализовать дизъюнкции (рисунок 5.5):

,

.

Для реализации булевых функций сведения о PLM должны быть представлены в определенной форме. Информацию о конкретной PLM принято представлять таблицей истинности.

	Рисунок 5.5-Упрощенная схема реализации  и  в PLM

 

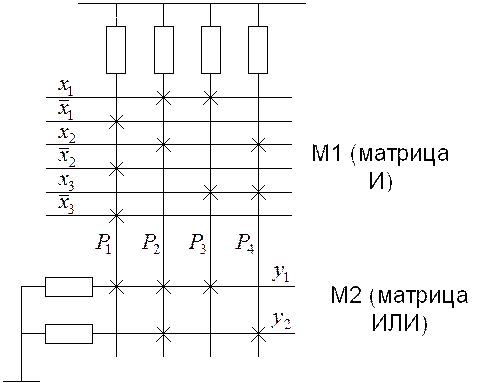
Таблица 5.1

Для взятого примера таблица имеет вид представленный в таблице 5.1.

Каждой промежуточной шине , , …, , …,  в соответствие ставится строка в таблице. На пересечении k-го столбца и i-той строки записывается "1", если  (k=1, 2, 3, …, s) входит в i-конъюнкцию без инверсии, и "0", если  входит в i-конъюнкцию с инверсией. Если  не входит в i-конъюнкцию, то ставится прочерк.

На пересечении i-той строки и j-того столбца (столбца выходной функции) записывается "1" если  конъюнкция входит в ДНФ функции , либо  *   , если  конъюнкция не входит в ДНФ.

Таблица истинности PLM используется при ее программировании. Для матрицы М1 сведения в таблице означают:

"1" – следует оставить целой перемычку прямого входа переменной и пережечь перемычку инверсного входа;

"0" – следует оставить целой перемычку инверсного входа и удалить прямого;

"–" – нужно пережечь перемычки обоих входов переменной.

Для матрицы М2 сведения в таблице истинности означают следующее: