Сравнить характеристики полученного фильтра с характеристиками фильтра, реализованного в пакете Filter Design программы MATHLAB.
.
Номер зачётки № 407269 ![]() Вариант №69
Вариант №69
![]()
![]() фильтр Баттерворта
фильтр Баттерворта
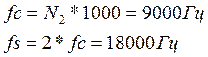
Рассчитать цифровой фильтр Баттерворта пятого порядка, методом билинейного z преобразования. Получить схему фильтра, его основные характеристики, а так же АЧХ и ФЧХ, групповое время задержки, импульсную характеристику. Все реализовать в программе MATHLAB.
3. Теория - Фильтр Баттерворта
Фильтры являются основой для большинства приложений обработки сигналов. Типичное назначение - это извлечение или вырезка области спектра входного сигнала или определенной частоты. Используемые для кондиционирования сигналов фильтры нередко называются частотно-селектирующими, поскольку обычно разрабатываются на основе требований к частотной характеристике.
Основное значение фильтра нижних частот (далее ФНЧ) - с
минимальным ослаблением передавать на выход колебания, частоты которых не превосходят
заданной граничной частоты, называемой частотой среза фильтра ![]() . В то же время колебания с
более высокими частотами должны существенно ослабляться.
. В то же время колебания с
более высокими частотами должны существенно ослабляться.
Очевидно, для ФНЧ с частотой среза ![]() идеальная частотная зависимость
коэффициента передачи мощности имеет вид:
идеальная частотная зависимость
коэффициента передачи мощности имеет вид:
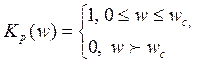
(имеются в виду физические частоты w>0).
Такая частотная характеристика заведомо нереализуема. Обращение в
нуль функции ![]() , а
значит и передаточной функции
, а
значит и передаточной функции ![]() противоречит известному критерию Пели – Винера.
противоречит известному критерию Пели – Винера.
Возникает задача подбора аппроксимирующей функции.
Один из возможных способов аппроксимации идеальной характеристики ФНЧ построен на использовании коэффициента передачи мощности
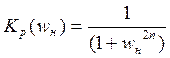 где
где ![]() - безразмерная
нормированная частота.
- безразмерная
нормированная частота.
ФНЧ, имеющий такие частотные свойства, называют фильтром с максимально-плоской характеристикой или фильтром Баттерворта. Целое число n=1,2,3,… является порядком фильтра. При любом n фильтр реализуем.
В полосе пропускания фильтра, т.е. при ![]() , квадрат модуля коэффициента передачи
плавно уменьшается с ростом частоты. На частоте среза ослабление, вносимое
фильтром, составляет - 3дБ независимо от порядка системы. Чем больше n,
тем точнее аппроксимируется идеальная форма частотной характеристики.
, квадрат модуля коэффициента передачи
плавно уменьшается с ростом частоты. На частоте среза ослабление, вносимое
фильтром, составляет - 3дБ независимо от порядка системы. Чем больше n,
тем точнее аппроксимируется идеальная форма частотной характеристики.
4. Расчет цифрового фильтра методом билинейного z преобразования
Данный метод позволяет синтезировать рекурсивный дискретный фильтр по частотной характеристике аналогового прототипа.
Функция передачи аналоговой цепи с сосредоточенными параметрами представляет собой дробно-рациональную функцию переменной s. Чтобы получить функцию передачи дискретного фильтра, необходимо перейти из s-области в z-область, причем дробно-рациональный характер функции должен сохраниться.
Поэтому замена для переменной s должна представлять собой также дробно-рациональную функцию переменной z. Чтобы частотные характеристики аналогового и дискретного фильтров были связаны простой зависимостью, искомая замена переменной должна отображать мнимую ось в s-области на единичную' окружность в z-области. В этом случае частотные характеристики аналогового и дискретного фильтров будут связаны лишь трансформацией частотной оси и никаких искажений «по вертикали» не будет.
Простейшей из функций, удовлетворяющих перечисленным требованиям, является билинейное z-преобразование (bilinear transformation):
Пусть нам дана передаточная функция для фильтра Батерворта пятого порядка:
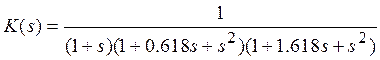
Коэффициент передачи
![]()
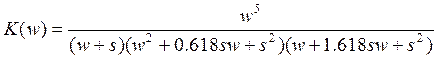
где ![]() Гц,
Гц,
![]() Гц
Гц
Подставляем w и получаем:
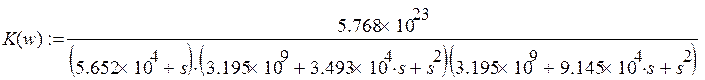
Принимаем 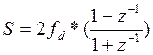
![]() Гц
Гц
Приведем полученное выражение к виду:
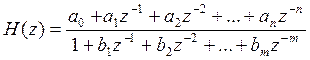
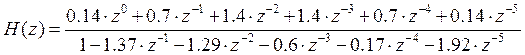
где,
ao = 0.14 bo = 1
a1 = 0.7 b1 = -1.37
a2 = 1.4 b2 = -1.29
a3 = 1.4 b3 = -0.6
a4 = 0.7 b4 = -0.17
a5 = 0.14 b5 = -1.92
Полученные коэффициенты используем для построения фильтра в программе MATHLAB.
5. Реализация фильтра в MATHLAB
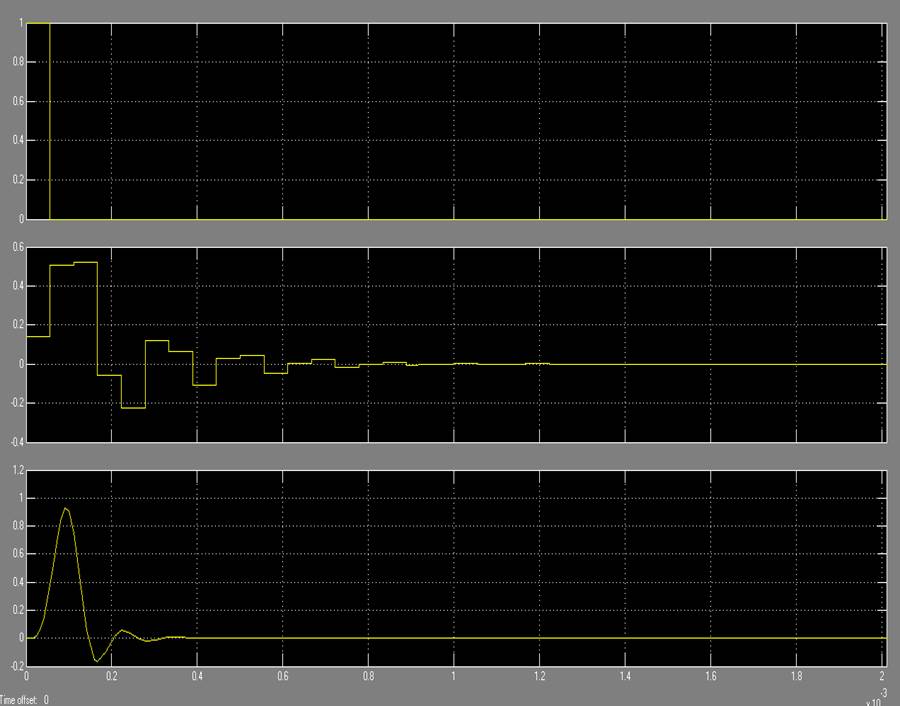
Для реализации фильтра в программе MATHLAB, используем прямую реализацию рекурсивного фильтра. (так как в схеме присутствуют обратные связи). При этом левая часть отображает числитель, а правая знаменатель. Количество усилителей соответствует количеству коэффициентов, а степень при z соответствует задержке. Все это подаем на сумматор, чтобы осуществлялась обратная связь. Результат на осциллографе.
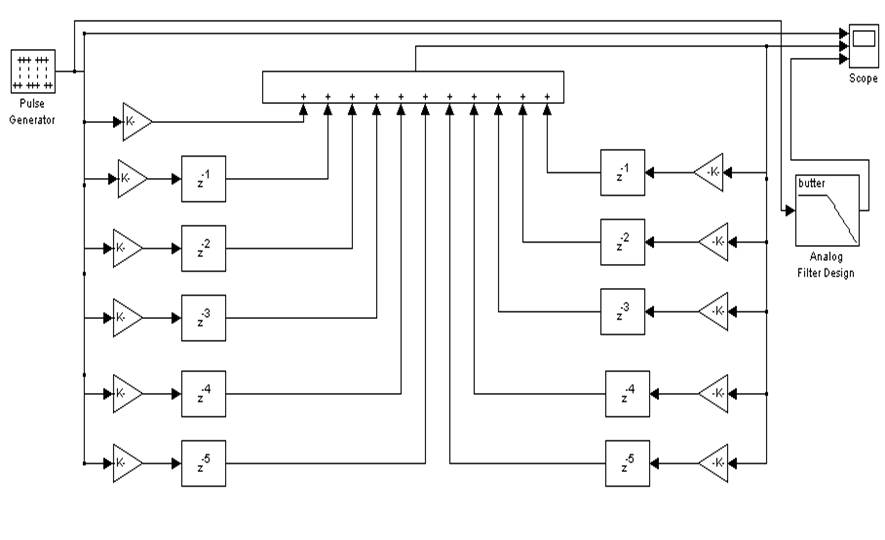
5.1. Элементы схемы
Осциллограф:
Сумматор:

Задержка:
Усилитель:
Генератор импульсов:
Аналоговый фильтр Баттерворта:
5.2. Полученные осциллограммы
6. АЧХ и ФЧХ, групповое время задержки, импульсная характеристика
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.