











































2 COMPUTATIONAL UNITS
Figure 2-0.
Table 2-0.
Listing 2-0.
This chapter describes the architecture and function of the ADSP-218x processors’ three computational units: the arithmetic/logic unit, the multiplier/accumulator and the barrel shifter.
Every device in the ADSP-218x family is a 16-bit, fixed-point processor. Most operations assume a twos-complement number representation, while others assume unsigned numbers or simple binary strings. Special features support multiword arithmetic and block floating-point. Details concerning the various number formats supported by the ADSP-218x family are given in Appendix A, “Numeric Formats”.
In ADSP-218x family arithmetic, signed numbers are always in twos-complement format. The processors do not use signed-magnitude, ones-complement, BCD or excess-n formats.
This is the simplest binary notation; sixteen bits are treated as a bit pattern. Examples of computation using this format are the logical operations: NOT, AND, OR, XOR. These ALU operations treat their operands as binary strings with no provision for sign bit or binary point placement.
Unsigned binary numbers may be thought of as positive, having nearly twice the magnitude of a signed number of the same length. The least significant words of multiple precision numbers are treated as unsigned numbers.
In discussions of ADSP-218x family arithmetic, “signed” refers to twos-complement. Most ADSP-218x family operations presume or support twos-complement arithmetic. The ADSP-218x family does not use signed-magnitude, ones-complement, BCD, or excess-n formats.
ADSP-218x family arithmetic is optimized for numerical values in a fractional binary format denoted by 1.15 (“one dot fifteen”). In the 1.15 format, there is one sign bit (the MSB) and fifteen fractional bits representing values from –1 up to one LSB less than +1.
Figure 2-1 shows the bit weighting for 1.15 numbers.
|
0 –2 |
–1 2 |
–2 2 |
–3 2 |
–4 2 |
–5 2 |
–6 2 |
–7 2 |
–8 2 |
–9 2 |
–10 2 |
–11 2 |
–12 2 |
–13 2 |
–14 2 |
–15 2 |
Figure 2-1. Bit Weighting for 1.15 Numbers
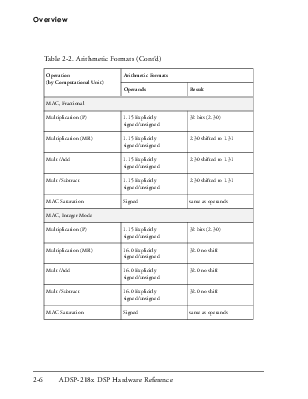
Table 2-1 gives examples of 1.15 numbers and their decimal equivalents:
Table 2-1. Examples of 1.15 Number Format
|
1.15 Number |
Decimal Equivalent |
|
0x0001 |
0.000031 |
|
0x7FFF |
0.999969 |
|
0xFFFF |
-0.000031 |
|
0x8000 |
-1.000000 |
All operations on the ALU treat operands and results as simple 16-bit binary strings, except the signed division primitive (DIVS). Various status bits treat the results as signed: the overflow (AV) condition code, and the negative (AN) flag.
The logic of the overflow bit (AV) is based on twos-complement arithmetic. It is set if the MSB changes in a manner not predicted by the signs of the operands and the nature of the operation. For example, adding two positive numbers must generate a positive result; a change in the sign bit signifies an overflow and sets AV. Adding a negative and a positive may result in either a negative or positive result, but cannot overflow.
The logic of the carry bit (AC) is based on unsigned-magnitude arithmetic. It is set if a carry is generated from bit 16 (the MSB). The (AC) bit is most useful for the lower word portions of a multiword operation.
The multiplier produces results that are binary strings. The inputs are
“interpreted” according to the information given in the instruction itself (signed times signed, unsigned times unsigned, a mixture, or a rounding operation). The 32-bit result from the multiplier is assumed to be signed, in that it is sign-extended across the full 40-bit width of the MR register set.
The ADSP-218x family supports two modes of format adjustment:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.