Преобразование Фурье для прямоугольных импульсов
, , г. Юбилейный, М.о.
Важным для понимания вопросов работы ключевого смесителя является знание коэффициентов разложения Фурье для спектральных составляющих прямоугольных импульсов.
При использовании прямоугольных импульсов в преобразователях частоты мы должны знать, на каких гармониках, кроме первой будет, происходить преобразование и с какой амплитудой. Наиболее широко в практике применяется управление ключами прямоугольными импульсами, длительность которых равна половине периода основной частоты. Такая последовательность импульсов называется меандром. Чтобы понять, почему происходит именно так, давайте посмотрим на примере спектра меандра.
На рис.1 представлена простая схема измерения, состоящая из генератора прямоугольных импульсов с частотой 1 МГц, скважность которых мы можем изменять, и осциллографа, на экране которого мы можем наблюдать форму импульсной последовательности. В окошке справа мы можем видеть, какие гармоники присутствуют в спектре меандра (Q=2), и какую они имеют амплитуду.
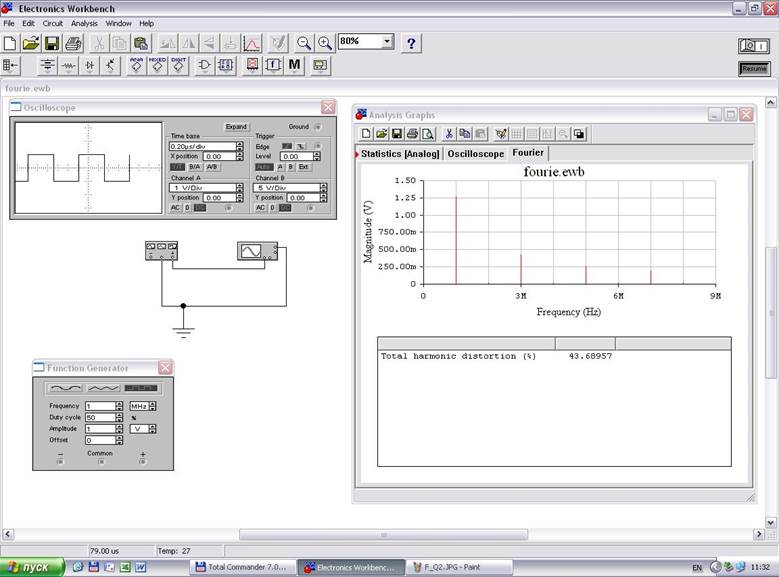
![]()
На что хочется обратить внимание? На экране осциллографа мы наблюдаем меандр с амплитудой от -1 до +1 В относительно нулевой линии. Т.е. размах амплитуды от пика до пика равен 2,0 вольта. В то же время на табло функционального генератора мы видим частоту 1 МГц, длительность импульса в 50% от периода следования, что соответствует Q=2, и амплитуду импульсов 1 В. На вкладке справа мы видим результат преобразования Фурье для первых 9 гармоник (это я так сам задал). Что же мы там видим? Постоянная составляющая полностью отсутствует. Это хорошо, т.к. наличие постоянной составляющей может влиять на смещение рабочей точки в реальном ключе, что нежелательно, т.к. чревато попаданием в нелинейную область АЧХ преобразующего элемента. Амплитуда 1-й гармоники равна примерно 1.26 В. Другими словами, коэффициент преобразования Фурье равен Кф1=1,26/2,0=0,63. Это приятно, т.к. мощность этой гармоники достаточно велика по сравнению с остальными гармониками. Как мы видим, 2-я гармоника представлена точкой около нуля. Это тоже приятно, т.к. при перемножении частот она не будет участвовать в формировании спектра сигналов на выходе смесителя. Аналогичную картину мы наблюдаем для 4, 6 и 8-й гармоники. Справедливости ради надо указать, что амплитуды четных гармоник всё же не равны нулю, а прибор показывает одинаковую для них амплитуду 0,013 В. Это в примерно в 97 раз меньше 1-й гармоники. А это почти на -40дБ. Практически такое соотношение позволяет пренебрегать четными гармониками.
Следующая значимая гармоника 3-я имеет амплитуду 0,43 В, что соответствует коэффициенту преобразования Фурье Кф3=0,43/2=0,215. Это тоже приятно, т.к. уровень этой гармоники в 2.93 раза меньше первой. Соответственно, во столько же раз слабее будут формироваться мешающие сигналы, проникающие на выход смесителя с этой частоты. Далее следует 5-я гармоника с амплитудой 0,255 В, Кф5=0,255/2=0,1275. Уже 7-я гармоника имеет уровень 0,187 В и Кф7=0,187/2=0,0935. 9-я гармоника отсутствует полностью. Чуть ниже там же приведен коэффициент гармонических искажений, равный 43,69%. Для прямоугольного сигнала это означает, что примерно 44% от мощности сигнала 1-й гармоники имеют все значимые гармоники, если мощность 1-й гармоники принять за 100%.
Следующим часто используемым является прямоугольный сигнал с Q=4. Какой при этом формируется спектр, представлено на рис.2.
![]()
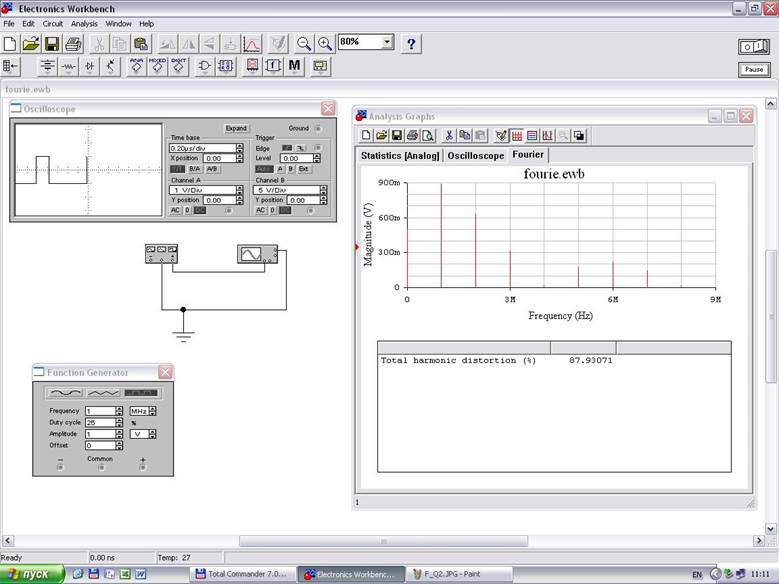
Отличия существенны и сразу заметны. Во-первых, появилась постоянная составляющая. Её амплитуда равна 0.51 В. А это уже не есть хорошо. Во-вторых, амплитуда 1 гармоники упала до 0,89 В. В третьих, появилась заметная 2 гармоника с амплитудой 0,64 В и 6 гармоника с амплитудой 0,22 В. 4 и 8 гармоники остались на прежнем уровне. 3, 5 и 7 гармоники имеют уровень 0,31, 0,175 и 0,149 В, соответственно. Ну что тут сказать? По 2 гармонике появился довольно внушительный канал паразитного приёма. Это означает, что нужно принимать дополнительные меры по ослаблению этого канала приёма.
Дальше начинается самое интересное. Существует мнение, что при укорочении импульсов можно получить
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.