Трассы с одиночным препятствием. Особенности реальных трасс. Построение профиля. Профиль трассы, страница 3

где 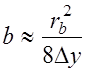   – радиус кривизны препятствия при r_b<<b    (см.     рис. 7.5).

Величина 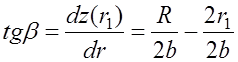  ,  откуда получим окончательное выражение

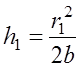, аналогично 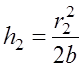   .                         (7.3.6)

Для удобства расчета выразим величины h₁ иh₂ через значения R, R₁, H и b.

Имея координаты двух точек для прямых АС -  (0, h₁); (r₁, z₁), и СВ - (R, h₂); (R-r₂, z₂), запишем уравнения их функций:

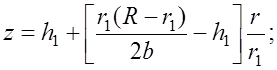                           (7.3.7)

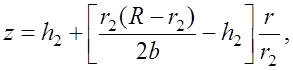                         (7.3.8)

где r- расстояние от соответствующего конца трассы до точки, где определяется величина z. Учитывая, что эти прямые пересекаются в точке С, расположенной на расстоянии R₁ от левого конца трассы, из (7.3.7) и (7.3.8) получим  первое уравнение для определения величин h₁ и h₂ через известные из профиля трассы значения R, R₁, H и b

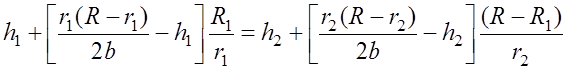.       (7.3.9)

Второе уравнение получим из геометрических выражений (из подобия треугольников АВС и АFG) по профилю (см. рис. 7.5):

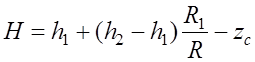,                       (7.3.10)

где z_c – высота точки С, которая может быть найдена из выражений (7.3.7) или (7.3.8) при соответствующих значения r=R₁ (r=R-R₁).  В результате, второе уравнение можно записать в виде

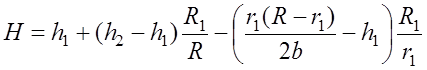.            (7.3.11)

Решая полученную систему уравнений (7.3.9), (7.3.11) с учетом формул (7.2.3) и (7.3.5), определим окончательные выражения

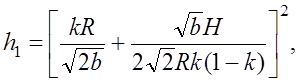                         (7.3.12)

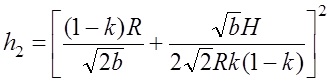.                    (7.3.13)

7.4.  Учет влияния рефракции на множитель ослабления

До сих пор рассматривались выражения при условии, что g=0. В реальных же условиях градиент диэлектрической проницаемости отличен от нуля, что приводит к рефракции волны, которую можно учесть заменой истинного на эквивалентный радиус Земли (a_Э)

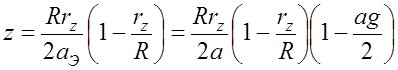.              (7.4.1)

Введение эквивалентного радиуса Земли позволяет трансформировать трассу (рис. 7.6), в результате чего произойдут изменения ее профиля, и, соответственно, ее параметров: .

 

Рис. 7.6.  Трансформация профиля при изменении

                                           условий  рефракции

Для избежания сложной процедуры трансформации трассы с небольшой погрешностью можно использовать приближенные выражения. Пологая, что, как правило, , в связи с чем значения  p  и m при трансформации трассы изменятся незначительно.

Радиус аппроксимирующей сферы препятствия b(g) приближенно можно выразить формулой

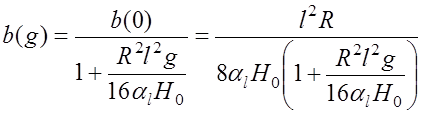,                     (7.4.2)

который можно получить из выражения (7.4.1) при k=1 (используя вместо a значение b) и несложных геометрических соображений.

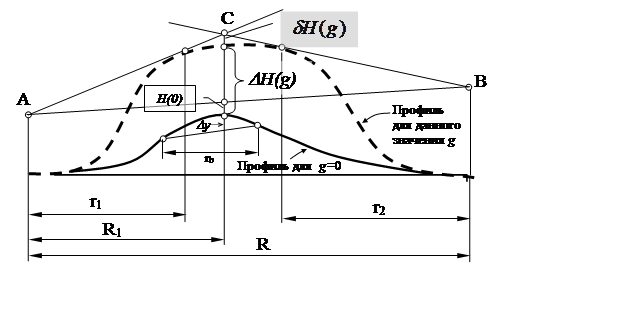
Значение высоты просвета H(g) при определенной величине g можно выразить через сумму (см. рис. 7.6):

,                   (7.4.3)

где H(0)- величина просвета при g=0, определяемая из профиля   (см. рис. 7.5); 

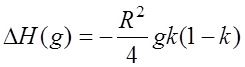, получено на основании формулы (7.4.1), как приращение высоты препятствия (z_Э(C) – z_C);

- высота точки С (см. рис. 6) над препятствием  при определенном значении g с учетом неравенств   и , можно определить из выражения

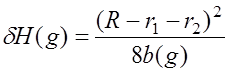,                              (7.4.4)

где

;    ,                   (7.4.5)

Заменяя в формулах (7.3.11) и (7.3.12) значения H на H(g) (7.4.3) и b на b(g) (7.4.2), получим уравнение, из решения которого определим  величину просвета с учетом рефракции

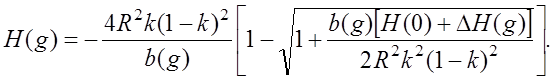          (7.4.6)

После подстановки вместо Н и b значений H(g) и b(g), определяемых формулами (7.4.2) и (7.4.6) получим следуещее выражение для  :

,                                 (7.4.6)

где 

;                             (7.4.7)

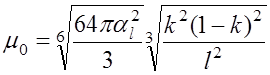;                          (7.4.8)

;

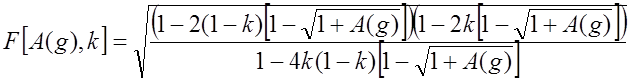(7.4.9)

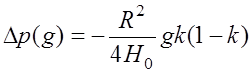;                          (7.4.10)

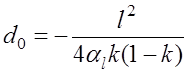;                                   (7.4.11)

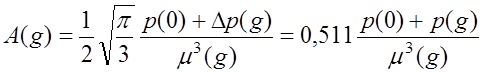;            (7.4.12)

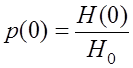.                                           (7.4.13)

С учетом формул (7.4.6), (7.4.10) - (7.4.13) выражение для относительного просвета можно записать в виде:

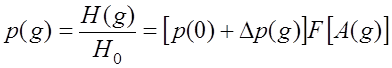,           (7.4.14)

где

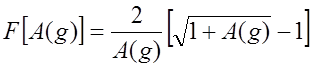.                       (7.4.15)

На рис. 7.7, 7.8 показаны графики функций  и .

 

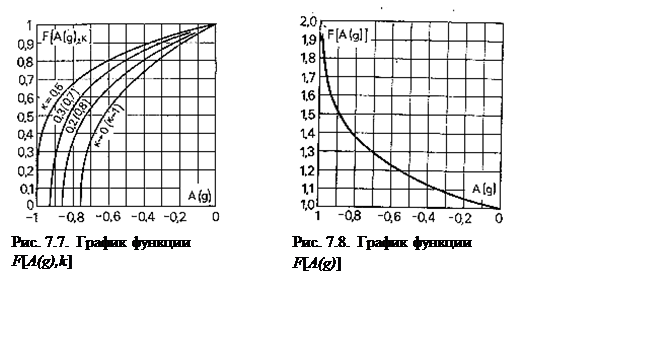При  из (7.4.14) и (7.4.15) величина относительного просвета приближенно определяется выражением

.                                (7.4.16)

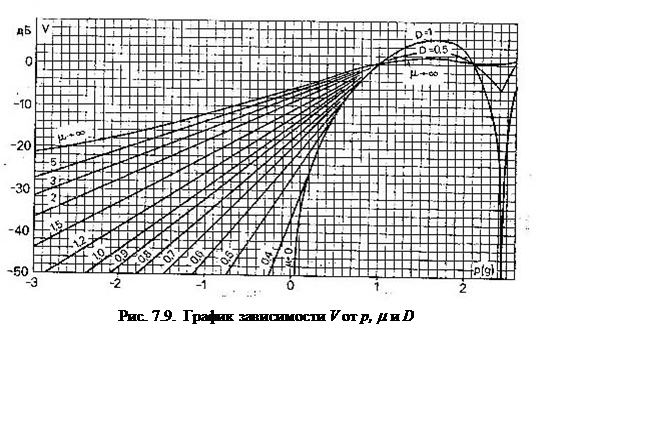На рис. 7.9 показаны зависимости V от p(g) при различных значениях параметра  в области  и коэффициента расходимости D в области  в предположении, что форма препятствия является выпуклой и гладкой.

Из анализа зависимости множителя ослабления (см. рис. 7.9) следует, что при  (трасса соответствует идеально плоским поверхностям), для которых , а при – трассам с клиновидным препятствием, когда имеет место переход к оптической дифракции Френеля. Значение V в области тени  в последнем случае оказывается значительно выше, чем для препятствий выпуклой формы с большим радиусом кривизны, поэтому клиновидное препятствие на трассе вызывает «эффект усиления препятствия».