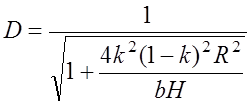Трассы с одиночным препятствием. Особенности реальных трасс. Построение профиля. Профиль трассы, страница 2

,    где b – радиус кривизны сферы, аппроксимирующей препятствие. Значения этого радиуса вычисляют по значениям  и , которые определяются из профиля трассы графически (см. рис. 4). Так как всегда выполнимо условие , то

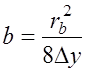.                                      (7.2.6)

С учетом выражения (7.2.6) коэффициент расходимости будет равен

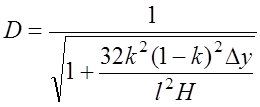,                            (7.2.7)

где 

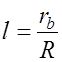.                                          (7.2.8)

В расчетах для удобства часто используется не абсолютной, а относительной величиной просвета

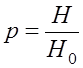,                                      (7.2.9)

где

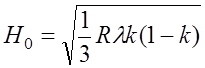                                  (7.2.10)

- величина просвета, соответствующая минимальной области пространства, в которой множитель ослабления равен единице.

Подставляя выражение (7.2.9) в (7.2.2) с учетом (7.2.10), получим

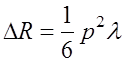,                                    (7.2.11)

в соответствии с чем множитель ослабления будет равен

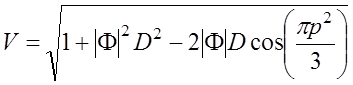.                  (7.2.12)

Из выражения (7.2.12) видно, что при p=1 сдвиг фаз между прямой и отраженной от препятствия волнами равен  (из-за малости , фазу коэффициента отражения можно считать равной ) и V=1 практически в независимости от . Таким образом, смысл величины просвета Н_o  заключается в том, что при  множитель ослабления по модулю равен примерно единице.

Из выражения множителя ослабления следует, что интерференционные максимумы и минимумы будут наблюдаться при p_m и  p_n, равных  соответственно:

                                  (7.2.13)

                                                 (7.2.14)

а абсолютные значения просвета, соответствующие m-му максимуму и n-му минимуму будут равны:

                    (7.2.15)

                     (7.2.18)

Чаще всего на реальных трассах угол скольжения достаточно мал и при относительно ровном профиле коэффициент отражения будет равен .  В этом случае значение интерференционного минимума можно вычислить

,                                          (7.2.19)

где  D_n – значение коэффициента расходимости для n-го минимума.

С учетом значения H_n в формуле (7.2.18), из выражений (7.2.7) и (7.2.19) получим, что

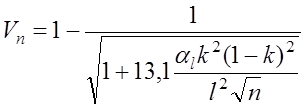,                      (7.2.20)

где

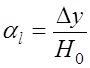.                                           (7.2.21)

Глубокие  интерференционные минимумы будут тогда, когда второе слагаемое под корнем в (7.2.20) существенно меньше единицы. В этом случае значение множителя ослабления для интерференционного минимума можно определить из приближенного выражения:

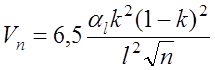 .                               (7.2.22)

Следует заметить, величина множителя ослабления критична к значению модуля коэффициента отражения. В связи с чем при наличии на трассе неровностей следует проверить выполняемость критерия Рэлея (6.2.17), который для n-го минимума с учетом формул (7.2.4) и  (7.2.16) можно записать в виде                      

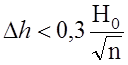.                                      (7.2.21)

Этот критерий должен проверятся в пределах минимальной зоны, охватывающей геометрическую точку отражения. Для реальной выпуклой поверхности размеры этой зоны с учетом формул (7.2.5) и (7.2.16) определяются выражениями:

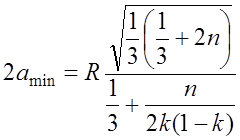;                             (7.2.22)

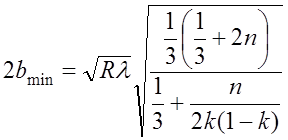.                      (7.2.23)

Из данных выражений следует, что величины  и  принимают наибольшие значения, если точка отражения лежит в середине трассы (k=0,5):

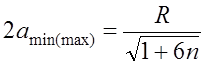;                          (7.2.24)

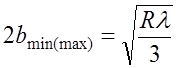.                               (7.2.25)

7.3.  Трассы с отрицательным просветом

В случае закрытых трасс, когда величина просвета отрицательна () для определения множителя ослабления используется дифракционная формула. На практике широко применяется приближенное выражение (6.4.2) для случая гладкой поверхности. Аналогичное выражение можно получить для случая реальной закрытой трассы, заменив радиус Земли на радиус кривизны  препятствия (рис. 7.5):

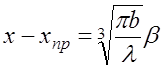,                                (7.3.1)

 

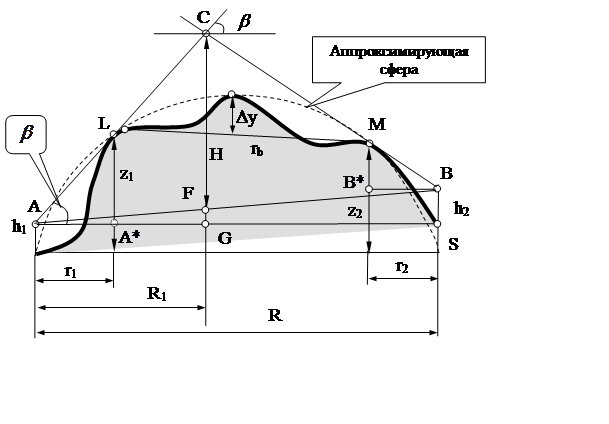Рис. 7.5.  К определению множителя ослабления при H<H₀

где b – средний радиус кривизны препятствия; 

-  угол дифракции

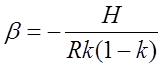.                               (7.3.2)

Множитель ослабления имеет линейную зависимость от величины просвета, которую можно получить из значений множителя в двух точках. Известно, что V=1(V=0 дБ) при H=H₀, а при H=0, множитель ослабления равен V=V₀. Откуда значение множителя ослабления будет определяться выражением

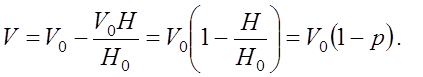            (7.3.3)

Значения m для реальных условий определяются из приведенных высот антенн, которые можно получить из следующих выражений, полученных из геометрических характеристик трассы            (см. рис. 7.5).

Величина , а .

Значения z₁ и z₂  можно получить из условия, что аппроксимируемая сфера описывается функцией параболы при :

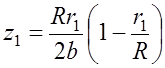,                                    (7.3.4)

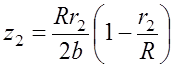,                                    (7.3.5)