 |
Лекция 7: ТРАССЫ С ОДИНОЧНЫМ ПРЕПЯТСТВИЕМ
План занятия:
Время |
№п/п |
Содержание раскрываемого вопроса: |
|
35 мин. |
1 |
Особенности реальных трасс. Построение профиля |
|
55 мин. |
2 |
Трассы с положительным просветом |
|
45 мин. |
3 |
Трассы с отрицательным просветом |
|
45 мин. |
4 |
Учет влияния рефракции на множитель ослабления |
7.1 Особенности реальных трасс. Построение профиля
Проведем анализ влияния рельефа местности для реальных трасс. Чаще всего, с учетом различных препятствий, радиус кривизны земной поверхности отличается от рассмотренного случая гладкой поверхности, имеющего значение эквивалентного радиуса Земли. Это оказывает значительное влияние на значение множителя ослабления.
Наиболее типичным вариантом являются трассы с одиночным ярко выраженным препятствием выпуклой формы (рис. 7.1).
|

Рис. 7.1. Профиль трассы
Вначале определим значение множителя ослабления, позволяющее учесть только влияние рельефа местности (без учета влияния рефракции в тропосфере, т.е. g=0 и aЭ=a).
Для возможности учета влияния рельефа местности на множитель ослабления необходимо иметь профиль трассы (см. рис. 7.1). Для удобства профили трасс строятся в прямоугольных координатах: расстояние наносится на оси абсцисс, а высота по оси ординат (а не по радиусу, как обычно). При таком построении профиля для сохранения соответствия высот точек линии АВ над уровнем моря линия, отображающая ее, должна иметь вид параболы
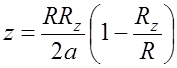 , (7.1.1)
, (7.1.1)
где R – протяженность трассы; Rz – расстояние от левого конца трассы до точки, в которой определяется величина z (см. рис. 7.1).
При построении профиля трассы вначале наносится линия нулевого уровня на протяжении от точки А до точки В. На профиле трассы отмечаются все возвышенности , лес и различные месные предметы (строения и пр.). Зная высоты подъема передающей и приемной антенн h1 и h2, проводится прямая линия АВ, соединяющая точки передачи и приема.
 Для определения множителя ослабления с учетом конкретного
профиля трассы удобнее пользоваться не значениями высот антенн h1
и h2, а величиной просвета H
между линией АВ и профилем трассы в наиболее высокой точке,
которая определяется графически непосредственно из профиля. В случае если
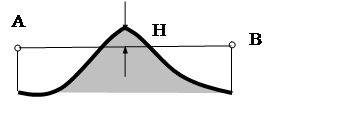
пространство между точками АВ на протяжении всей трассы открыто, просвет
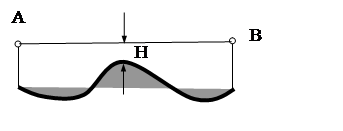
называют положительным (рис. 7.2), а при закрытом, каким либо препятствием –
отрицательным (рис. 7.3).
Для определения множителя ослабления с учетом конкретного
профиля трассы удобнее пользоваться не значениями высот антенн h1
и h2, а величиной просвета H
между линией АВ и профилем трассы в наиболее высокой точке,
которая определяется графически непосредственно из профиля. В случае если
пространство между точками АВ на протяжении всей трассы открыто, просвет
называют положительным (рис. 7.2), а при закрытом, каким либо препятствием –
отрицательным (рис. 7.3).
|
||||
|
||||
7.2 . Трассы с положительным просветом
Если значение просвета H на трассе с одиночным препятсвием положительно и достаточно велико, то
в точку приема будут приходить две волны: прямая и отраженная от препятствия
(рис. 4). В этом случае для вычисления множителя ослабления можно воспользоваться
полученным интерференционным выражением, лишь с заменой разности хода волн ![]() , угла скольжения
, угла скольжения ![]() и коэффициента
расходимости D, учитывающих конкретный профиль трассы.
и коэффициента
расходимости D, учитывающих конкретный профиль трассы.
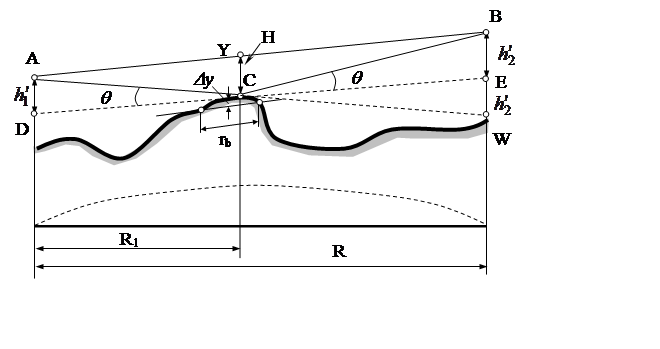 |
положительным просветом
Из геометрии трассы получим значение разности
хода волн. В реальных условиях наклон линии АВ
незначителен, поэтому треугольники ACD и BCE можно приближенно считать прямоугольными, а величину ![]() . При таких условиях
. При таких условиях
![]() . (7.2.1)
. (7.2.1)
Так как ![]() и
и
![]() , то разлагая подкоренные
значения в (7.2.1) в биномиальные ряды и используя только первые два члена
разложения, данное выражения можно привести к виду
, то разлагая подкоренные
значения в (7.2.1) в биномиальные ряды и используя только первые два члена
разложения, данное выражения можно привести к виду
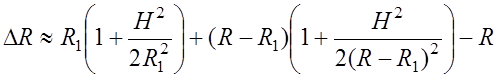
![]()
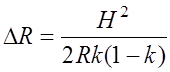 , (7.2.2)
, (7.2.2)
где 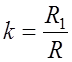 . (7.2.3)
. (7.2.3)
При тех же условиях приближения угол скольжения можно определить из подобия треугольников АСD и CBE:
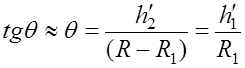 , выразив
значение
, выразив
значение ![]() через H из подобия
треугольников АBW и АСY (см.
рис. 7.1):
через H из подобия
треугольников АBW и АСY (см.
рис. 7.1): 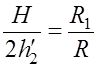 , получим
окончательное выражение
, получим
окончательное выражение
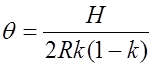 . (7.2.4)
. (7.2.4)
Значения приведенных высот антенн над плоскостью, касательной к профилю в точке отражения определяются аналогично (см. рис. 1), конечные выражения для которых имею вид:
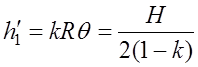 ;
; 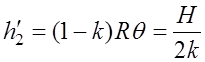 . (7.2.5)
. (7.2.5)
Подставив выражения (7.2.5) в формулу коэффициента расходимости D, получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.