 |
4 часа
Лекция 3: ВЛИЯНИЕ АТМОСФЕРЫ НА РАСПРОСТРАНЕНИЕ
РАДИОВОЛН В ЗОНЕ ПРЯМОЙ ВИДИМОСТИ
План занятия:
Время |
№п/п |
Содержание раскрываемого вопроса: |
|
30 мин. |
1 |
Существенная область однородного пространства, влияющая на распространение радиоволн |
|
15 мин. |
2 |
Пространственно-временные изменения диэлектрической проницаемости тропосферы |
|
45 мин. |
3 |
Рефракционные свойства земной атмосферы. Уравнение траектории волны |
3.1. Существенная область однородного пространства, влияющая на
распространение радиоволн
При распространении радиоволн в однородном безграничном пространстве различные ее области неодинаково влияют на процесс распространения радиоволн, т.е. имеется некоторая существенная область, которая оказывает определяющее влияние на данный процесс.
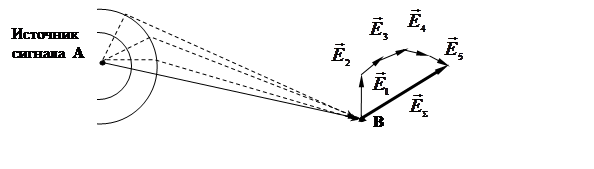
Согласно принципу Гюйгенса-Френеля формируемое поле в произвольной точке приема, есть результат векторного сложения от виртуальных источников, расположенных в некоторой замкнутой поверхности (рис. 3.1).
 |
![]()
По мере удаления от линии, соединяющей излучатель и точку приема, интенсивность излучения виртуальных источников умень,шается как из-за увеличения расстояния до излучателя, так и за счет диаграмм направленности. В этой связи область пространства, оказывающая существенное влияние на процесс распространения радиоволн в однородной безграничной среде, есть эллипсоид вращения с фокусами в точках передачи и приема (рис. 3.2). Сечение этого эллипсоида плоскостью, перпендикулярной линии АВ, дает окружность (существенную зону), называемую в зависимости от размеров определенной зоной Френеля.
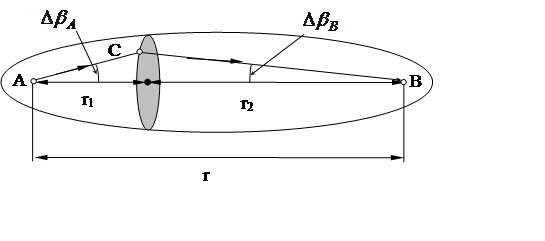 |
Рис. 3.2. Существенная область пространства
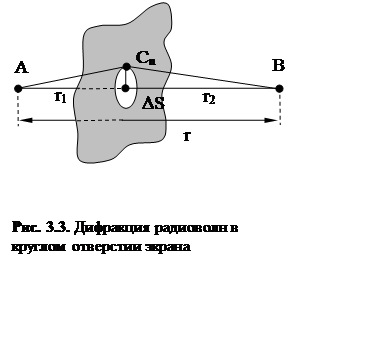 Если
между излучателем и точкой приема установить перпендикулярно оси АВ непрозрачный
экран с отверстием в точке С (рис. 3.3), то отношение напряженности
поля в точке приема
Если
между излучателем и точкой приема установить перпендикулярно оси АВ непрозрачный
экран с отверстием в точке С (рис. 3.3), то отношение напряженности
поля в точке приема 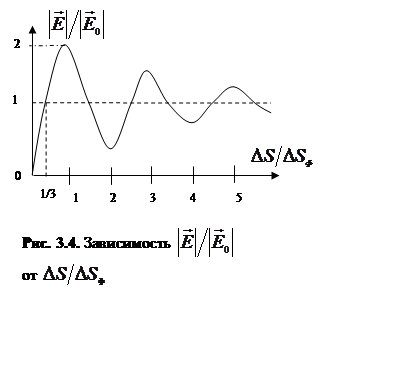
Определим радиусы зон Френеля, каждый из
которых соответствует разности хода волны по двум траекториям: АВ и АСnВ,
которая отличается половиной длины волны ![]() .
Данное условие можно записать как
.
Данное условие можно записать как
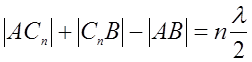 , (3.1.1)
, (3.1.1)
которое можно выразить из прямоугольных треугольников через расстояния до зоны Френеля (см. рис. 3.2, 3.3):
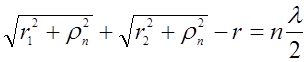 . (3.1.2)
. (3.1.2)
Подкоренные выражения можно разложить в ряд
Бинома, используя только первые два члена, так как 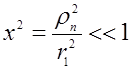 :
:
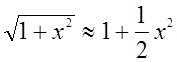 .
.
То есть можно
записать 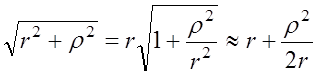 , откуда
, откуда
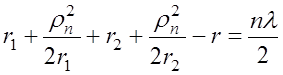 , следовательно
, следовательно
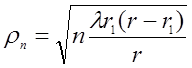 , (
, (![]() ). (3.1.3)
). (3.1.3)
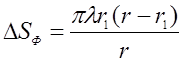 . (3.1.4)
. (3.1.4)
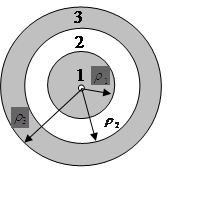 |
Из формулы (3.1.3) видно, что максимальный радиус зоны Френеля достигается при r1=r2=r/2 и уменьшается по мере приближения к точкам А и В (см. рис. 3.2).
Из рис.
3.4 видно, что для радиусов зон Френеля с нечетным номером соответствует
максимумы отношения ![]() , а
четным минимумы. Причина заключается в том, что происходит сложение и вычитание
полей от всех виртуальных источников расположенных в пределах незатененных зон
Френеля.
, а
четным минимумы. Причина заключается в том, что происходит сложение и вычитание
полей от всех виртуальных источников расположенных в пределах незатененных зон
Френеля.
По мере увеличения радиусов с увеличением номера зоны Френеля напряженность поля изменяется незначительно, поэтому существенная область ограничена 8-10 зонами. Дальнейшее увеличение вызывает изменение лишь 20% напряженности поля.
Кроме понятия существенной области
пространства, вводится понятие минимальной области, которая представляет собой
эллипсоид вращения. Радиусу сечения минимальной зоны соответствует отношение ![]() , и это соответствует
, и это соответствует ![]() . Радиус минимальной
зоны в плоскости экрана равен
. Радиус минимальной
зоны в плоскости экрана равен
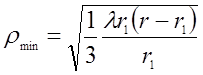 . (3.1.5)
. (3.1.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.