Влияние атмосферы на распространение радиоволн в зоне прямой видимости. Существенная область однородного пространства, влияющая на распространение радиоволн, страница 3

3.2.  Рефракционные свойства земной атмосферы.

Уравнение траектории волны

Для достаточно удаленных радиотрасс, использующих поверхностные волны, существенное влияние оказывает рефракционное воздействие тропосферы в диапазоне метровых, дециметровых и сантиметровых волн.

Как показано выше, с изменением высоты тропосферы происходит изменение диэлектрической проницаемости, что, в свою очередь приводит к изменению траектории радиоволны, это вызывает так называемое явление рефракции. Данное явление необходимо учитывать для радиотрасс большой протяженности на расстояниях 30 и более километров.

Для получения аналитических выражений, определяющих рефракционные свойства тропосферы, проведем анализ траектории волны.  Тропосферу с изменяющей диэлектрической проницаемостью представим в виде слоистой структуры по высоте, где скачкообразно изменяются ее параметры (рис. 3.6), где величина dh® 0.

Согласно второму закону преломления Снелля, при прохождении волны через среды с различной диэлектрической проницаемостью происходит изменение траектории этой волн, что выражается изменением угла падения на тропосферу (см. рис. 3.6):

.                                                                                                                      (3.3.1)

Преобразуем данное выражение с учетом условий: dh®0 Þ de®0, .  Откуда получим

В данном выражении использовано приближение, соответствующее вышепринятым условиям:     .  Раскрывая скобки, получим

в котором  бесконечно малая величина. В результате для нашего случая формула (3.3.1) запишется

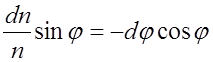,                                                                                                                                        (3.3.2)

или выразив через e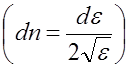,выражение (3.3.2) запишется

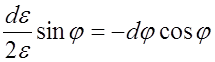.                                                                                                                                      (3.3.3)

Учитывая изменение траектории волны на небольшом участке (в пределах dh)  дугу  ab можно считать прямой линией (см. рис. 3.6).  Определим радиус кривизны траектории на этом участке по геометрическим формулам

.                                                                                                                                                    (3.3.4)

Определим зависимость углов падения от высоты слоя dh из треугольника abc:

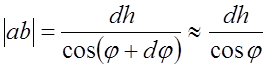.                                                                                                                                           (3.3.5)

Тогда подставляя выражение (3.3.4) в (3.3.5) получим

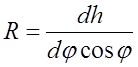,                                                                                                                                               (3.3.6)

после подстановки этой формулы в (3.3.3) определим окончательное выражение для радиуса кривизны траектории волны (что является уравнением траектории волны):

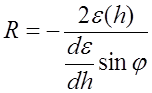.                                                                                                                                               (3.3.7)

Учитывая линейную зависимость диэлектрической проницаемости на рассматриваемых радиотрассах (3.2.5) и с учетом, что , выражение (3.3.7) преобразуется в вид

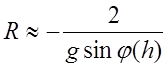.                                                                                                                                                 (3.3.8)

Полагая, что в используемых радиотрассах начальные углы падения волны равны , выражение (3.3.8) примет вид

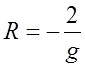,                                                                                                                                                   (3.3.9)

т.е. при линейном изменении  траектория волны будет представлять дугу, радиус которой определяется градиентом диэлектрической проницаемости воздуха g.

При линейном изменении eсуществует возможность использовать эквивалентный радиус Земли а_Э исходя из условий:

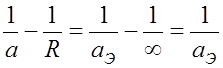, откуда

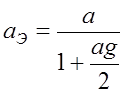.                                                                                                                                                    (3.3.9)

Полученное выражение (3.3.9) значительно облегчает расчет радиотрасс. В этом случае, пользуясь эквивалентным радиусом Земли,  можно использовать модель без учета рефракции в атмосфере.

При линейной зависимости  различают следующие виды рефракции (рис. 3.7):

1.  Отрицательную рефракцию и субрефракцию при , в этом случае   и .

2.   Положительную рефракцию, соответствующую значениям , при этом  и .

3.  Критическую рефракцию, возникающую при 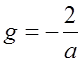, когда  и .

4.  Сверхрефракцию, когда 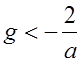, когда  и .

 

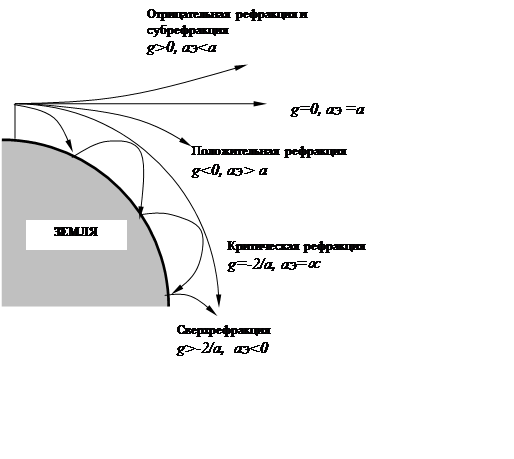Рис. 3.7.  Виды рефракции радиоволн в атмосфере