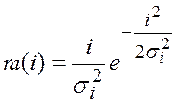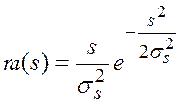Оценка эффективности приема имитопомех во время сеанса связи. Оценка эффективности имитоатаки каналов с постоянными параметрами, страница 5

;            ;           , где – среднеквадратическое отклонение ортогональной составляющей уровня имитопомехи; – среднеквадратическое отклонение ортогональной составляющей уровня полезного сигнала; – среднеквадратическое отклонение ортогональной составляющей уровня шума. При этом каждую случайную величину можно разложить на ортогональные составляющие, имеющие нормальное распределение, сумма соответствующих значений которых также будет иметь нормальное распределение (рис. 5.30). Для приведенного случая:

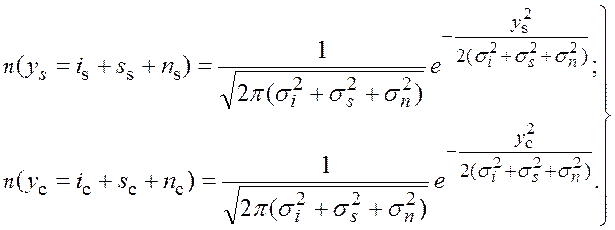
Исходя из данных условий, суммы соответствующих случайных величин в каждом частотном подканале будут иметь рэлеевское распределение [51]. Для первого случая:

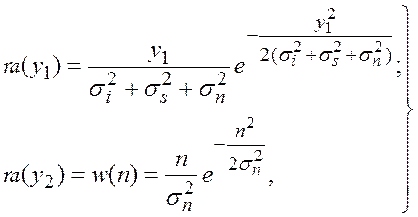                   (5.37)

и для второго случая:

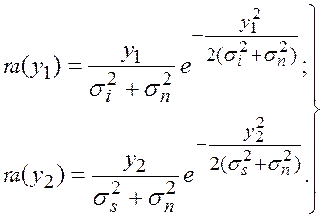                   (5.38)

Откуда определим вероятность ошибки I рода [145]:

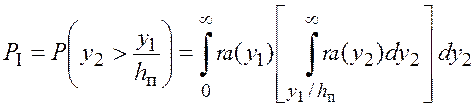,             (5.39)

где – пороговое отношение уровней имитопомехи к сигналу, обеспечивающее допустимые краевые искажения [см. формулу (5.13)].

Подставим выражения (5.37) в формулу (5.39):

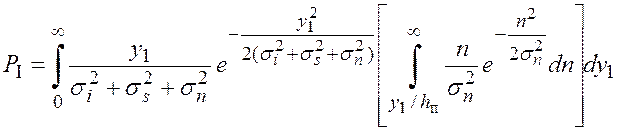.      (5.40)

Вычислим данное выражение поэтапно:

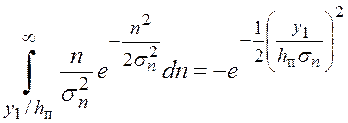, откуда, получим:

.

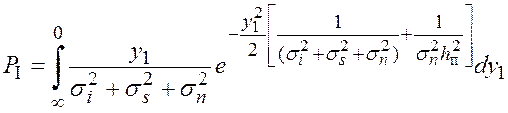Решим данный интеграл методом подстановки:

, 

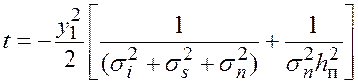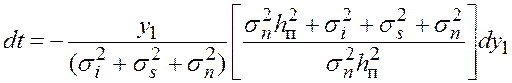, откуда

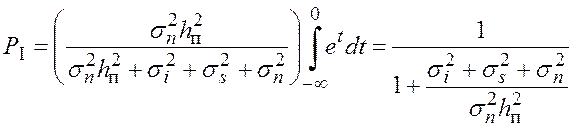          (5.41)

или с учетом распределения отношения уровней имитопомехи к полезному сигналу, подробный анализ которого рассмотрен в разделе 6.4.1, [114]

.

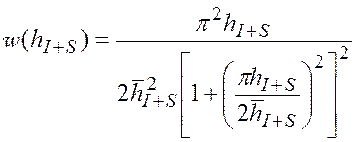выражение (5.41) примет вид:

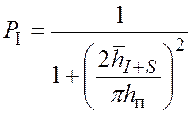,                                    (5.42)

где  – математическое ожидание отношения суммарного сигнала к шуму; .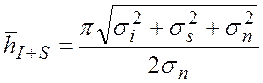

Аналогично, с учетом формулы (5.38), получим оценку вероятности ошибки II рода [145]:

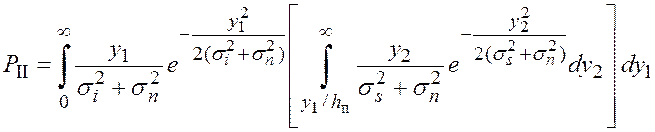.  (5.43)

Вычислим данное выражение поэтапно:

, с учетом полученного выражения

.

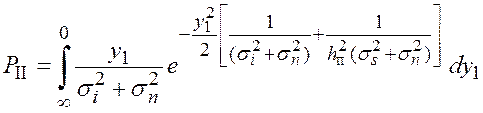Вычислим данный интеграл методом подстановки:

,

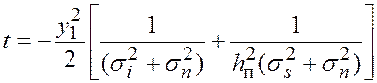, на основании чего

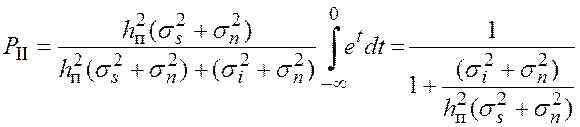 ,       (5.44)

и с учетом плотности распределения

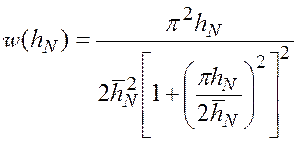, выражение (5.41) примет вид

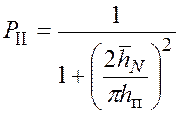,                                       (5.45)

где – математическое ожидание отношения суммы имитопомехи с шумом к сумме полезного сигнала с шумом; .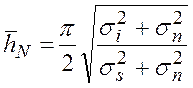

Далее после подстановки выражений (5.42) и (5.45) в формулу (5.36) получим оценку вероятности ошибки приема элемента имитопомехи в каналах с рэлеевскими замираниями при частотной манипуляции:

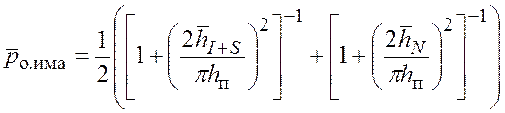.              (5.46)

В этом случае следует заметить, что при больших значениях уровня полезного сигнала (характерно для действующих каналов связи) значение , что позволяет в выражении (5.46) с небольшой погрешностью пренебречь значением первого слагаемого, в результате чего окончательное выражение для вероятности ошибки имитоатаки примет вид (рис. 5.31):

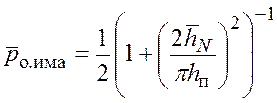.                                (5.47)

Как видно из рис. 5.31, с увеличением соотношения уровней имитопомехи к полезному сигналу повышается эффективность имитоатаки, однако влияние замираний и шумов эфира существенно повышает требуемое соотношение  относительно граничного значения  [см. раздел 5.1]. Жирной линией показана эффективность имитоатаки, при которой обеспечивается прием посылок имитопомехи без краевых искажений, а в случае допуска краевых искажений эффективность имитоатаки возрастает.

Для анализа зависимости (5.47) от уровня шумов проанализируем величину :

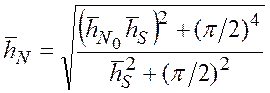,                                     (5.48)

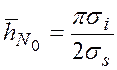где – математическое ожидание отношения уровней имитопомехи к полезному сигналу при отсутствии шумов; ;  – математическое ожидание отношения уровней полезного сигнала к шуму; .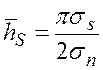

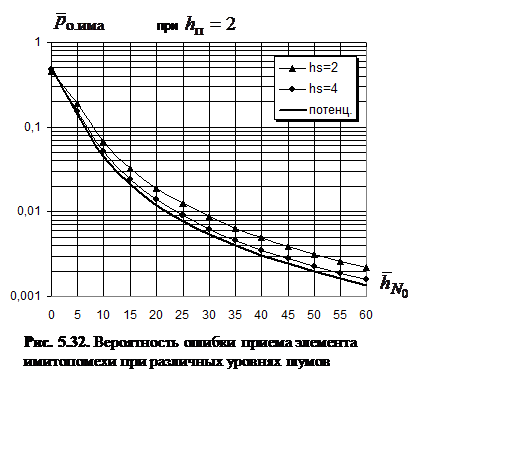
При  . Иллюстрация данной тенденции показана в зависимости  на рис. 5.32, из которой видно, что при снижении уровня шумов (с ростом ) эффективность имитоатаки приближается к потенциальной (предельным возможностям имитоатаки при отсутствии шумов). Учитывая высокую помехоустойчивость действующих систем связи, для оценки эффективности имитоатаки каналов с замираниями можно использовать приближенное выражение

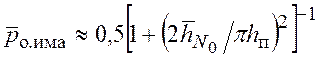.                                (5.49)