Оценка эффективности приема имитопомех во время сеанса связи. Оценка эффективности имитоатаки каналов с постоянными параметрами, страница 3

Определим интегральную функцию распределения совместного события суммы двух случайных величин [см. формулу (5.25)], обобщенное выражение которого в случае их независимости имеет вид [51]

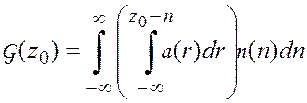.                             (5.26)

В нашем случае область определения двух случайных величин имеет ограничения ,   (рис. 5.27), в связи с чем пределы интегрирования в выражении (5.26) будут изменены:

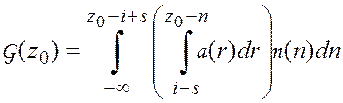.                            (5.27)

Подставив выражения плотностей вероятности в формулу (5.27), произведем вычисление интеграла:

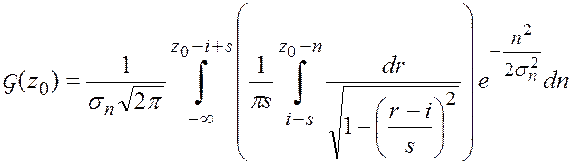.      (5.28)

Произведем поэтапный расчет интеграла:

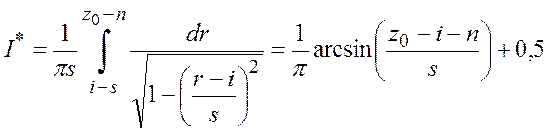.      (5.29)

Подставив полученное выражение (5.29) в формулу (5.28), получим

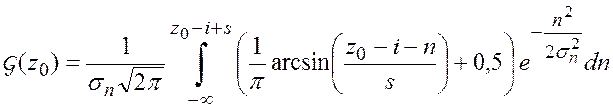.   (5.30)

При  вычислении  интеграла  следует  учесть, что  область   определения    функции 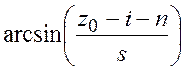 ограничена значениями аргумента  (см. рис. 5.27). При  значение случайной величины  ограничено: , что соответствует значениюI^*=1. С учетом рассмотренных ограничений выражение (5.30) можно записать:

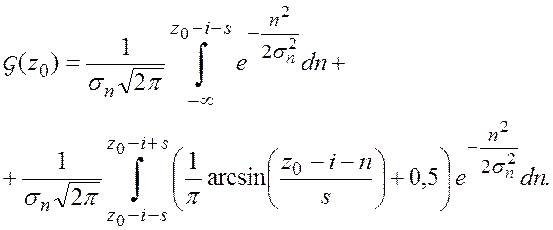
Вычислим каждый интеграл отдельно:

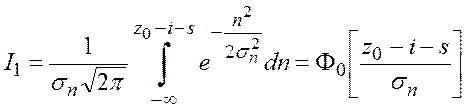, где  – табулированная функция Крампа; .

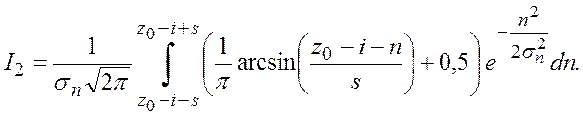    (5.31)

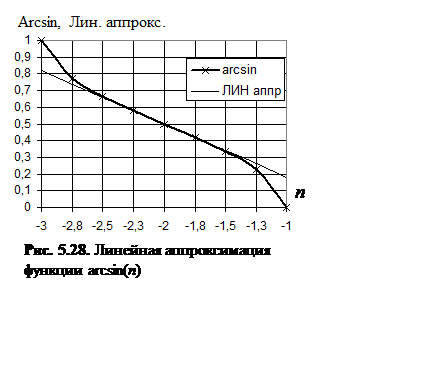
Непосредственно вычислить данный интеграл в аналитическом виде затруднительно, в связи с чем для упрощения расчетов осуществим линейную аппроксимацию функции 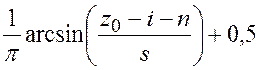 на интервале  (рис. 5.28). В данном интервале значений n аргумент функции  будет ограничен величиной , что позволяет с определенной долей погрешности воспользоваться для аппроксимации приближением , которое справедливо для достаточно малых значений аргумента.

В результате аппроксимирующее выражение примет следующий вид:

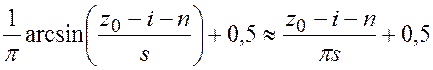.               (5.32)

Воспользовавшись полученным приближением (5.32), вычислим выражение (5.31):

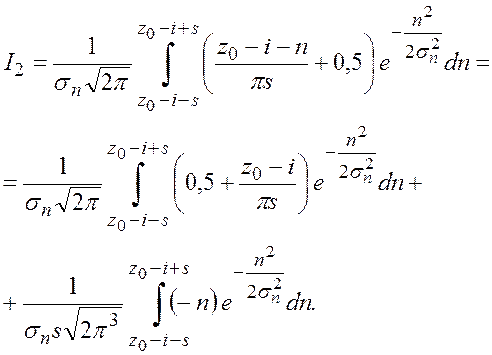
Произведем расчет каждого интеграла поэтапно:

.

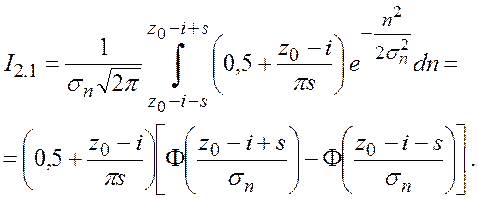
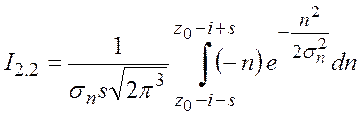Вычислим этот интеграл методом подстановки: 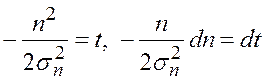, исходя из чего

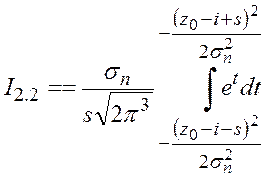, откуда

.

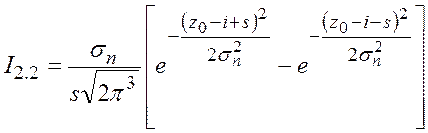В результате окончательное выражение для интегральной функции распределения совокупности случайных величин будет иметь вид

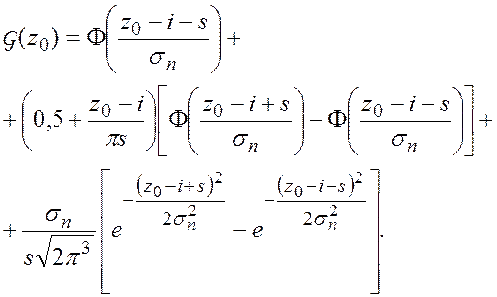
Введем следующие обозначения: 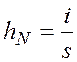; ; 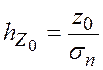, с учетом которых

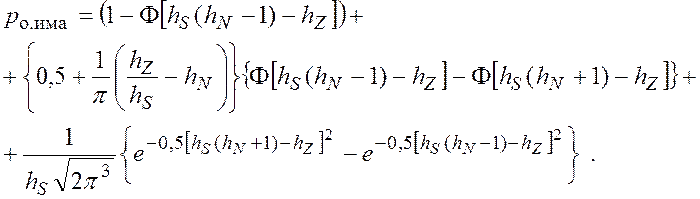  (5.33)

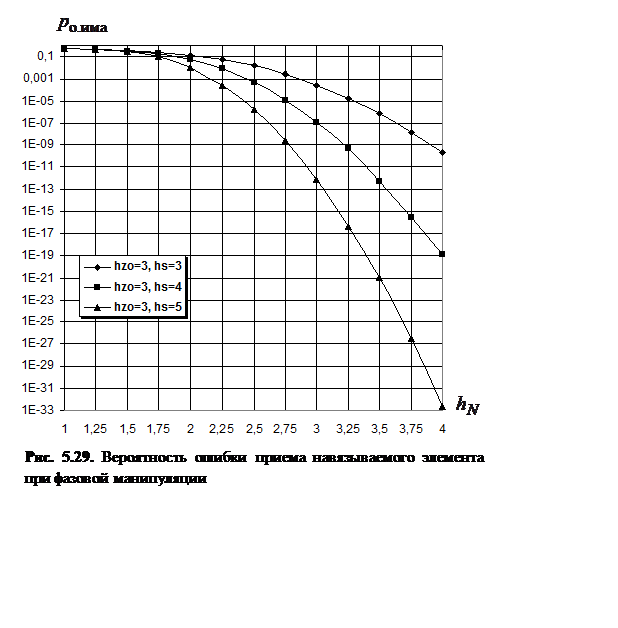
Полученное выражение является оценкой вероятности ошибки приема элемента навязываемого сигнала в канале с постоянными параметрами при наличии гауссовского шума (рис. 5.29). Из данного рисунка видно, что в худших условиях приема при  эффективная имитоатака достигается при повышенных значениях отношения уровней имитопомехи к полезному сигналу: . В случае большего уровня полезного сигнала  устойчивый прием имитопомехи обеспечивается при меньших значениях : .

С учетом того, что в каналах с постоянными параметрами реальные соотношения уровней имитопомехи и полезного сигнала могут находиться в пределах , при которых первое и последнее слагаемые выражения (5.33) более чем на порядок меньше второго, с достаточной точностью для инженерных расчетов можно использовать приближенное выражение

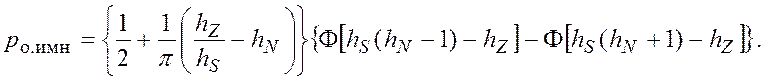 (5.34)

5.2.2. Оценка  эффективности имитоатаки каналов с замираниями

При использовании декаметровых каналов и радиолиний дальней тропосферной связи УКВ диапазона возможности имитоатаки во время сеансов связи определяются, прежде всего, особенностями прохождения радиоволн. В этих каналах наблюдается многолучевое отражение радиоволн, в результате которого происходят регулярные изменения амплитудных и угловых параметров принимаемого сигнала [33], что существенно снижает эффективность использования когерентных способов приема [38, 145]. Наиболее устойчивый прием в этих каналах обеспечивается при использовании частотной манипуляции с некогерентным  способом обработки сигнала, получившей наибольшее применение в действующих системах связи. На основании этих особенностей для оценки эффективности имитоатаки рассмотрим модель воздействия имитопомех на радиоканалы с частотной манипуляцией. Для анализа данной модели необходимо учесть возникающие при распространении радиоволн изменения амплитудных и угловых параметров принимаемого сигнала и воздействие гауссовского шума. При используемых скоростях манипуляции изменения параметров сигнала вызывают медленные замирания амплитуды с плотностью распределения Рэлея [33, 38]