Оценка эффективности приема имитопомех во время сеанса связи. Оценка эффективности имитоатаки каналов с постоянными параметрами, страница 2

Определим функцию распределения суммы имитопомехи и полезного сигнала . При этом следует учесть, что практически во всех современных РПУ используется автокорреляционный прием, помехоустойчивость которого при достаточном превышении сигнала над помехой приближена к возможностям когерентного приема, исходя из чего, при анализе следует учитывать только синфазную составляющую суммарного сигнала r (рис. 5.22):

,                                 (5.19)

где  – амплитуда имитопомехи;  – амплитуда полезного сигнала.

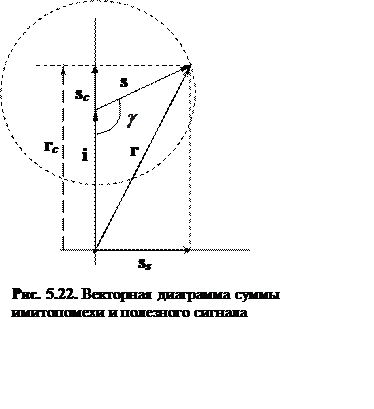Из формулы (5.19) выразим амплитуду синфазной составляющей суммарного сигнала

,                                          (5.20)

на основе которой определим функцию плотности ее распределения.

Для определения закона распределения проанализируем функцию  на интервале  (рис. 5.23). Данная функция немонотонна в установленном интервале и является четной.

Для определения функции плотности распределения суммарного сигнала следует найти вероятность того, что его амплитуда не превысит некоторое значение . Такое требование будет выполнено при условии, когда  и  (см. рис. 5.23), откуда с учетом четности функции (5.17) и известной функции распределения фазового сдвига (5.16) получим

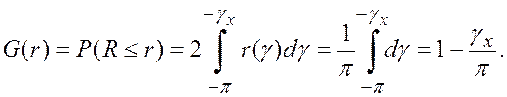              (5.21)

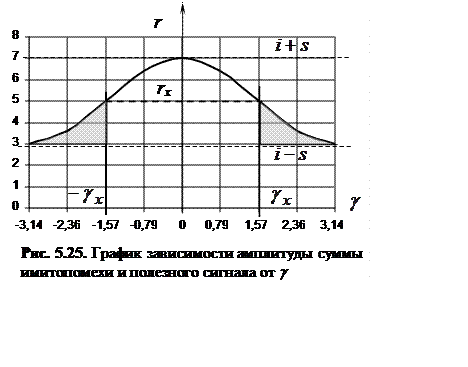Из формулы (5.20) выразим величину  через параметр :

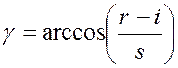.                                          (5.22)

Подставив выражение (5.22) в формулу (5.21), определим функцию плотности распределения, соответствующую распределению арксинуса:

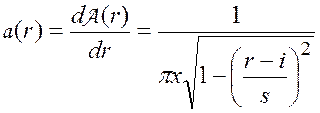.                         (5.23)

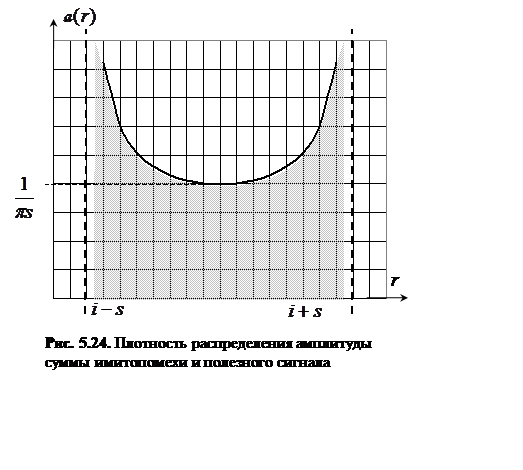
С учетом того, что , область определения функции (5.23) будет также ограничена  (рис. 5.24). В данном случае, если пренебречь влиянием шумов эфира, что характерно для случая ближней связи при больших отношениях сигнал-шум, полученное выражение плотности распределения (5.23) можно использовать для оценки эффективности имитоатаки, которую можно выразить через вероятность ошибки приема одной элементарной посылки имитопомехи:

,

где – чувствительность приемного устройства.

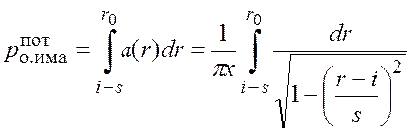Вычислим данный интеграл методом подстановки . В результате получим окончательное выражение

.

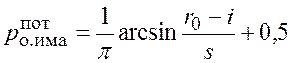Обозначив 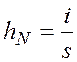, , 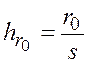получим выражение вида

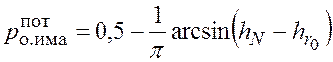.                           (5.24)

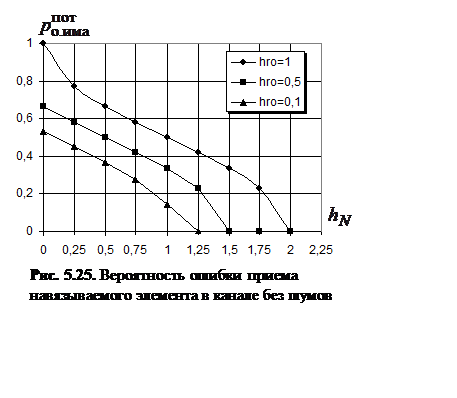
Графики данной функции показаны на рис. 5.25, из которого видно, что при отсутствии шумов в канале связи в наихудшем случае при  эффективность приема элемента имитопомехи обеспечивается при . В случае более высокого уровня полезного сигнала эффективность имитоатаки достигается при меньших значениях .

В реальных каналах связи всегда необходимо учитывать влияние шумов эфира, в связи с чем представленную оценку в формуле (5.24) можно использовать только как предельно возможную для оценки потенциальной имитостойкости канала связи. Для оценки влияния шумов рассмотрим комбинацию полученной случайной величины rсовместно со случайным гауссовским шумом n. Аналогично первому случаю рассмотрим вариант когерентного приема, вследствие чего необходимо учесть только синфазные составляющие суммы сигнала r и  шума n (рис. 5.26):

,

т. е. необходимо рассмотреть комбинацию суммы двух случайных величин:

.            (5.25)

Причем следует учесть, что ортогональные составляющие амплитуды шума распределены по нормальному закону [51], вследствие чего для получения совместного закона распределения необходимо использовать законы:  и  .

В конечном итоге необходимо получить оценку вероятности ошибки приема элемента сигнала в условиях гауссовского шума, которая совпадает с выражением для интегральной функции распределения совместной вероятности для значения  , равного чувствительности приемного устройства:

.