Решение обыкновенных дифференциальных уравнений. Разработка алгоритмов и проектировка программного обеспечение для численного решения обыкновенных дифференциальных уравнений

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО

Факультет автоматизированных и информационных систем

Кафедра «Информационные технологии»

ЛАБОРАТОРНАЯ РАБОТА №4

по дисциплине: «ЧИСЛЕННЫЕ МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ»

Решение обыкновенных дифференциальных уравнений

Выполнил:   студент гр. ИТ-31

Принял:        доцент

Гомель 2015

Лабораторная работа №4

«Решение обыкновенных дифференциальных уравнений»

Цель работы: научиться разрабатывать алгоритмы и проектировать программное обеспечение для численного решения обыкновенных дифференциальных уравнений.

Разработать алгоритм и написать программу, реализующую численного решение обыкновенных дифференциальных уравнений следующими методами.

5. Милна.

// ConsoleApplication2.cpp: определяет точку входа для консольного приложения.

//

#include "stdafx.h"

#include <iostream>

#include <math.h>

#include <iomanip>

using namespace std;

double f(double x, double y)

{

       return x+cos(y);

}

int _tmain(int argc, _TCHAR* argv[])

{

       setlocale(LC_ALL, "Russian");

       int choose = 0;

       double a = 1.8, b = 2.8;

       while (choose != 7)

       {

             cout << "Меню:" << endl;

             cout << "1)Метод Адамса" << endl;

             cout << "2)Метод Милна" << endl;

             cout << "Выберите пункт меню: ";

             cin >> choose;

             double x0 = 1.8, y0 = 2;

             switch (choose)

             {

             case 1:

             {

                            const int n = 10000;

                            double x[n + 1], y[n + 1], y1;

                            double h = (b - a) / n;

                            y[0] = y0;

                            for (int i = 0; i <= n; i++)

                            {

                                   x[i] = x0 + i*h;

                            }

                            for (int i = 0; i < 3; i++)

                            {

                                   y[i + 1] = y[i] + h*(f(x[i] + h / 2, y[i]) + h / 2 * (f(x[i], y[i])));

                            }

                            for (int i = 3; i < n; i++)

                            {

                                   y1 = y[i] + h * (-9 * f(x[i - 3], y[i - 3]) + 37 * f(x[i - 2], y[i - 2]) - 59 * f(x[i - 1], y[i - 1]) + 55 * f(x[i], y[i])) / 24;

                                   y[i + 1] = y[i] + h*(f(x[i - 2], y[i - 2]) - 5 * f(x[i - 1], y[i - 1]) + 19 * f(x[i], y[i]) + 9 * f(x[i + 1], y1)) / 24;

                            }

                            cout << "y=" << setprecision(15) << y[n] << endl;

             }

                    break;

             case 2:

             {

                            const int n = 10000;

                            double x[n + 1], y[n + 1], y1;

                            double h = (b - a) / n;

                            y[0] = y0;

                            for (int i = 0; i <= n; i++)

                            {

                                   x[i] = x0 + i*h;

                            }

                            for (int i = 0; i < 3; i++)

                            {

                                   y[i + 1] = y[i] + h*(f(x[i] + h / 2, y[i]) + h / 2 * (f(x[i], y[i])));

                            }

                            for (int i = 3; i < n; i++)

                            {

                                   y1 = y[i-3] + 4*h * (2 * f(x[i - 2], y[i - 2]) - f(x[i - 1], y[i - 1]) + 2 * f(x[i], y[i])) / 3;

                                   y[i + 1] = y[i - 1] + h*(f(x[i - 1], y[i - 1]) + 4 * f(x[i], y[i]) + f(x[i + 1], y1)) / 3;

                            }

                            cout << "y=" << setprecision(15) << y[n] << endl;         

             }

                    break;

             default:

             {

                             cout << "Неверно!" << endl;

             }

                    break;

             }

       }

       fflush(stdin);

       return 0;

}

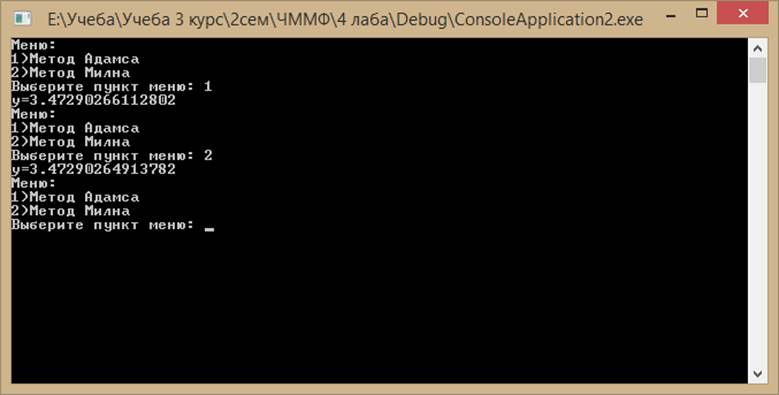
Ход выполнения работы:

Вывод: в ходе лабораторной работы были реализованы алгоритмы численного решения обыкновенных дифференциальных уравнений такие как метод Рунге–Кутта четвертого порядка, метод Адамса, метод Хорда, модифицированный метод Эйлера, метод Милна, метод Кутта-Мерсона. Был проведен анализ данных методов, в ходе которого выявлено что при большом количестве разбиений методы дают одинаковые значения с относительно небольшой погрешностью. Однако следует отметить, что наиболее точными методами является метод Кутта-Мерсона, метод Адамса.