МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
«Гомельский государственный технический университет имени П. О. Сухого»
Факультет автоматизированных и информационных систем
Кафедра «Информационные технологии»
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №3
по дисциплине «Численные методы математической физики»
на тему: «Решение параболических уравнений методом конечных разностей»
|
Выполнил: студент группы ИТ-32 |
|
|
|
|
|
Проверил преподаватель: |
|
|
|
|
|
Дата сдачи отчета __________________ |
|
|
Дата допуска к защите ______________ |
|
|
Дата защиты ______________________ |
Гомель 2013
Цель: реализовать алгоритм решения параболических уравнений методом конечных разностей.
Задание:
Решить ДУЧП нестационарной задачи теплопроводности, используя явную двухслойную схему метода конечных разностей. Начальные и граничные условия, а также правая часть дифференциального уравнения приведены в таблице. Величины L и T задать самостоятельно. Построить трехмерный график искомой функции u(x,t) для области 0<x<L и 0<t<T.
|
№ вар |
Граничные условия |
Начальные условия u(x,0) |
f(x,t) |
L |
T |
|
|
u(0,t) |
u(L,t) |
|||||
|
19 |
sin(2t+3) |
– |
|
– |
||
Ходработы:
Листинг ParabolicEquationSolver.cs
namespace Lab3.Classes
{
/// <summary>
/// Класс, реализующий решение параболического
/// уравнения методом конечных разностей
/// </summary>
class ParabolicEquationSolver
{
private double coreLength; // Длина стержня
private double time; // Временной интервал
private short xSplitCount; // Количество разбиений по х
private short tSplitCount; // Количество разбиений по t
private double heatSpendCoefficient; // Коэффициент теплопроводности
private double[,] decisions; // Матрица решений
/// <summary>
/// Конструктор с параметрами
/// </summary>
/// <param name="_coreLength">Длина стержня</param>
/// <param name="_time">Временной интервал</param>
/// <param name="_xSplitCount">Количество разбиений по х</param>
/// <param name="_tSplitCount">Количество разбиений по t</param>
/// <param name="_heatSpendCoefficient">Коэффициент теплопроводности</param>
public ParabolicEquationSolver(
double _coreLength, double _time,
short _xSplitCount, short _tSplitCount,
double _heatSpendCoefficient
)
{
coreLength = _coreLength;
time = _time;
xSplitCount = _xSplitCount;
tSplitCount = _tSplitCount;
heatSpendCoefficient = _heatSpendCoefficient;
ToSolve();
}
/// <summary>
/// Получение матрицы решений
/// </summary>
public double[,] GetDecisions { get { return decisions; } }
/// <summary>
/// Начальная граница
/// </summary>
/// <param name="t">Время</param>
/// <returns>Значение функции за время t</returns>
private double StartBorder(double t)
{
return System.Math.Sin((2 * t + 3) * System.Math.PI / 180);
}
/// <summary>
/// Конечная граница
/// </summary>
/// <param name="x">Длина</param>
/// <param name="t">Время</param>
/// <returns>Значение функции за время t на расстоянии x</returns>
private double EndBorder(double x, double t)
{
return 0;
}
/// <summary>
/// Начальные условия
/// </summary>
/// <param name="x">Длина</param>
/// <returns>Значение функции на растоянии x</returns>
private double EntryConditions(double x)
{
return System.Math.Sqrt(x * x * x + 2 * x + 5);
}
/// <summary>
/// Решение параболического уравнения
/// </summary>
private void ToSolve()
{
double xStep = coreLength / xSplitCount;
double tStep = time / tSplitCount;
decisions = new double[xSplitCount, tSplitCount];
for (int i = 0; i < xSplitCount; i++)
{
decisions[i, 0] = EntryConditions(i * xStep);
}
for (int j = 0; j < tSplitCount; j++)
{
decisions[0, j] = StartBorder(j * tStep);
decisions[xSplitCount - 1, j] = EndBorder(0, j * tStep);
}
double gamma = (heatSpendCoefficient * heatSpendCoefficient * tStep) / (xStep * xStep);
for (int j = 0; j < tSplitCount - 1; j++)
{
for (int i = 1; i < xSplitCount - 1; i++)
{
decisions[i, j + 1] = gamma * decisions[i + 1, j] + (1 - 2 * gamma) * decisions[i, j] + gamma * decisions[i - 1, j];
}
}
}
}
}
Тесты:
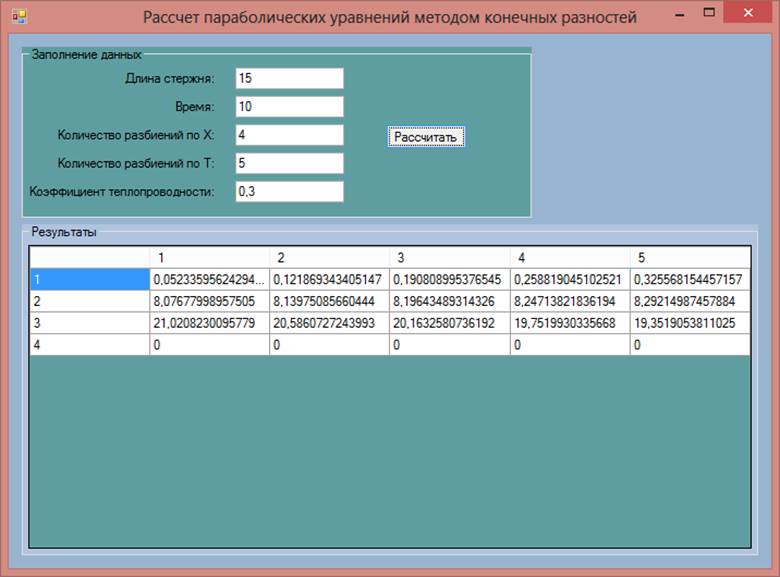
Рисунок 1 – Главное окно программы
Выводы: в ходе лабораторной рабы были изучены алгоритм метода конечных разностей, было разработано приложение для решения параболических уравнений методом конечных разностей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.