Общие сведения о дифференциальных уравнениях. Решение дифференциальных уравнений методами Рунге-Кутт

Метод LU разложения с единицами на главной диагонали матрицы U. Идея метода заключается в следующем [1].

Представим систему (1.1) в матричном виде

(1.15)

где  – квадратная матрица порядка n.

Представим матрицу A в виде где  – нижняя треугольная матрица, а  – верхняя треугольная матрица с единичной диагональю:

,

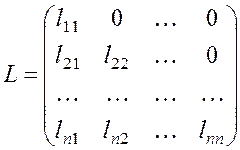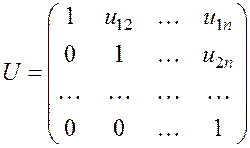
Тогда элементы  и  определяются по формулам:

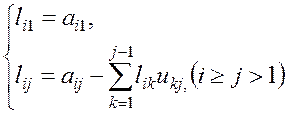(1.16)

и

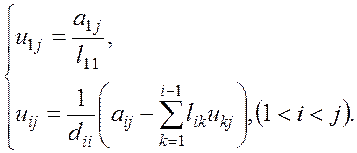(1.17)

Следовательно, вектор x можно вычислить из системы

 (1.18)

причем она легко решается, так как матрицы L и U – треугольные:

Алгоритм LU разложениядовольно прост и изображен на рис. 1.3.

Метод LU разложения с единицами на главной диагонали матрицы L. Представим матрицу  в виде произведения треугольных матриц и

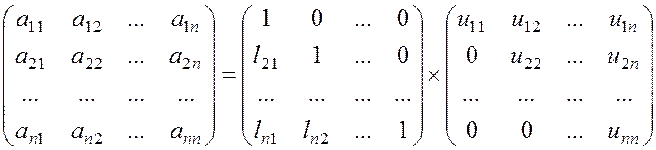
где элементы  и  определяются по формулам:

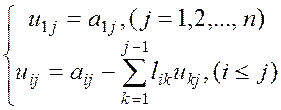(1.22)

и

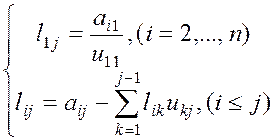(1.23)

Формулы(1.22) и (1.23) дают нам LU-разложение матрицы А. Итак ,если , то можно записать уравнение, эквивалентное (1.21):

(1.24)

Введем вектор вспомогательных переменных  и представим уравнение (1.24) в виде системы:

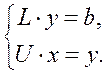
Таким образом, решение системы (1.1) с квадратной матрицей коэффициентов сводится к решению двух систем с треугольными матрицами коэффициентов:

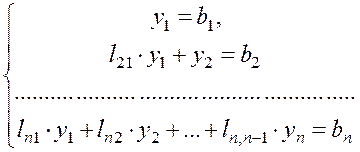(1.25)

и

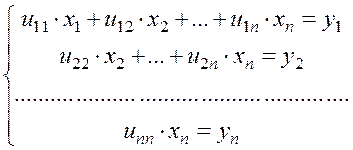(1.26)

Из (1.25) и (1.26) понятно, что все у_i могут быть вычислены по формуле:

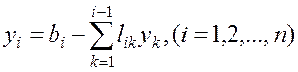,(1.27)

а для всех  истинно равенство

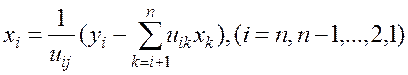(1.28)

Алгоритм решения системы линейных алгебраических уравнений с помощью LU-разложения приведен на рисунке 1.4

Метод ортогонализации. Заключается он в том, что систему (1.1) ортонормируют, то есть приводят ее к виду:

(1.29)

где Q – ортогональная матрица. Для этого разделим первое уравнение системы (1.1) на выражение

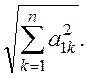
Получим

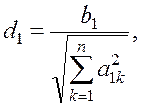
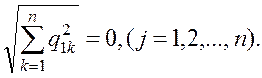  (1.30)

Тогда для второго уравнения системы (1.29) имеем:

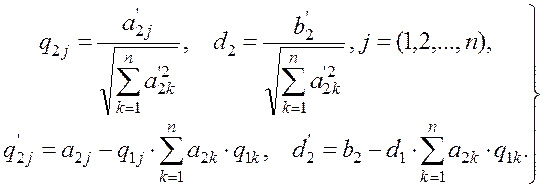
Следовательно, уравнение с номером i примет вид:

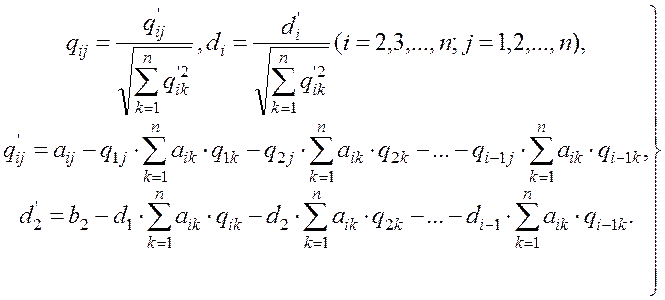(1.31)

Если система(1.1) совместна, то, воспользовавшись формулами (1.30) и (1.31), можно перейти к новой системы (1.29) где матрица Q будет ортогональной, а это значит, что она будет обладать свойством:

,

Где Е единичная матрица. Значит, решение системы (1.29) можно записать в виде:

, или

.

Рисунок 1.5 содержит алгоритм решение линейной системы методом отогонализации по формулам (1.30) ,(1.31) и (1.32). Заметим, что этим алгоритмом можно воспользоваться, если необходимо решить задачу вычисления ортогональной матрицы Q для матрицы А. Понятно, что в этом случае расчет вектора d теряет смысл.

Метод прогонки. На практике часто встречаются линейные системы вида:

,

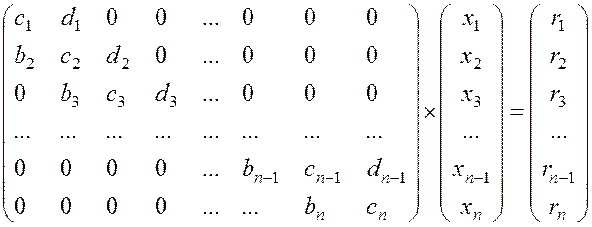которые называют системами с трехдиагональной матрицей коэффициентов. Каждое уравнение такой системы связывает три неизвестных, расположенных особым образом, и может быть записано в общем виде так:

(1.33)

где i=1, 2, n,  = 0, d_n = 0. Такие уравнения называют трехточечными разностными уравнениями второго порядка. Для решения систем (1.33) существует специальный метод, называемый методом прогонки. Заключается он в следующем [2]. Предположим, что существуют такие наборы чисел (i = 1, 2, ..., n), для которых

(1.34)

Уменьшим индекс в уравнении (1.34) и подставим его в (1.33), получим

, откуда имеем

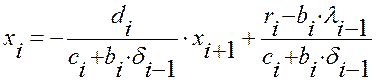
Следовательно, уравнение (1.34) имеет место, если для всех i= 1, 2, ...n, выполняются рекуррентные соотношения:

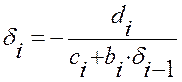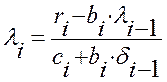,  (1.35)

Нетрудно заметить что, так как , то процесс вычисления   по формулам (1.35) можно начать со значений

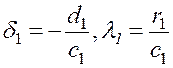
и продолжать для i= 1, 2,...,n. В случае, когда i = n и  d_n = 0, получим , то есть для i = n будем иметь

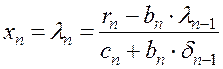
где  и  были вычислены на предыдущем шаге. Далее по формулам (1.35) последовательно находятся значения , , … ,  при i=n-1, n-2, …, 1.

Итак, алгоритм метода прогонки (рис. 1.5) сводится к вычислениям по трем формулам:

1. Находят прогоночные коэффициенты  по формулам (1.35). Этот процесс называют прямой прогонкой

2. Определяются неизвестные по формуле (1.34), выполняя тем самым обратную прогонку.

1.3. Приближенные методы решения систем линейных уравнений

Метод итерации. Разрешим первое уравнение системы (1.1) относительно , второе — относительно  и так далее. Получим систему, эквивалентную данной

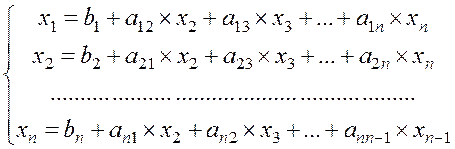(1.37)

где

  , 

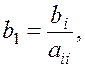
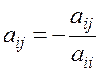(1.38)

Запишем систему (1.37) в матричном виде

(1.39)

где

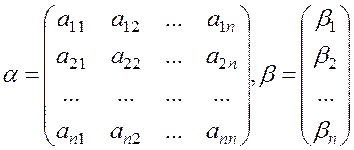
Для решения системы (1.39) методом итерации необходимо выбрать нулевое приближение. Пусть это будет столбец свободных коэффициентов

(1.40)

тогда первое приближение будет иметь вид:

а второе будет таким:

и так далее: (k + 1)-е приближение будем вычислять по формуле:

или в развернутом виде:

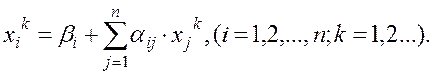(1.41)    

Вообще говоря, если последовательность приближений  имеет предел 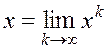, то этот предел и является решением системы (1.39).

При практическом применении метода итерации вычисления прекращают, когда выполняется условие

(1.42)

где  – заданная точность вычислений.

Приведем без доказательства условие сходимости метода итерации [1]: для существования единственного решения системы (1.36) и сходимости метода простых итераций достаточно выполнения условия

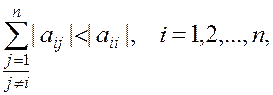(1.43)

то есть чтобы модули диагональных коэффициентов для каждого уравнения системы были больше суммы модулей всех остальных коэффициентов, не считая свободных.

Итак, алгоритм метода простой итерации (рис. 1.12) заключается в следующем:

1. Проверка условий (1.43), если они не выполняются, то работа алгоритма завершена, иначе переходим к п.2.

2. Формирование матрицы  и массива  по формулам (1.38).

3. Формирование начального приближения х⁰ по (1.40).

4. Расчет нового приближения  по (1.41).

5. Если условие (1.42) выполняется и максимальная ошибка вычислений меньше заданного числа e, то решение  найдено, иначе переходим к п.4.

Метод Зейделя. Представляет собой модификацию метода простой итерации. Основная идея [1] этого метода заключается в том, что при вычислении -го приближения неизвестной x_i учитываются уже вычисленные к этому времени -е предшествующих неизвестных

Пусть дана приведенная линейная система

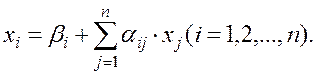(1.44)

Выберем в качестве начального приближения корней вектор

(1.45)

Тогда, согласно идее метода Зейделя, предполагая, что -е приближения корней известны, будем строить-е приближения по следующим формулам:

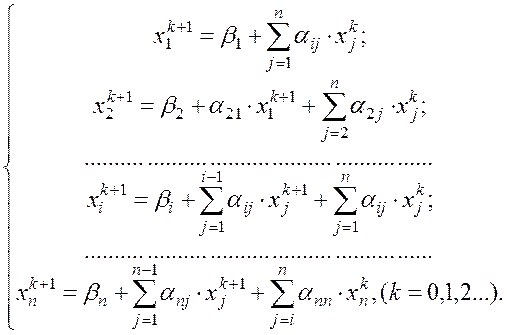(1.46)

Возникает вопрос о сходимости метода. Заметим, что условия (1.43) применимы и для метода Зейделя, кроме того, если линейная система (1.36) — нормальная, то процесс Зейделя для эквивалентной ей приведенной