Построение и исследование динамических моделей технических систем. Описание математической модели

Исследовать влияние значений изменяемого параметра на амплитуду перемещения груза, для этого рассчитать функцию перемещения движения груза при различных значениях изменяемого параметра. Построить графики зависимости перемещения груза от времени.

3.       Построить сводный график всех полученных функций перемещения на одном поле.

4.       Построить график зависимости локального экстремума перемещения от варьируемого параметра.

5.       Вычислить аналитические аппроксимирующие функции по результатам исследований предыдущего пункта. Построить графически исходные и аппроксимирующие зависимости. Сделать выводы по проведенным исследованиям.

Индивидуально технические объекты (вариант 3)

Исходными данными для задачи являются:

x0 – отклонение груза от положения равновесия в начальный момент времени;  m – масса груза;  с – жесткость пружин; a – коэффициент вязкого сопротивления жидкости, таблица 1,2.

Таблица 1 – Исходные данные

Варьируемый параметр	C (кн/н)	m (кг)	a (H·c·м-1)	x0	tк  (с)
m	3,1	50	500	0.03	1

Таблица 2 – Варьируемый параметр

m

50

70

100

115

130

150

170

190

215

Описание математической модели

Дан прибор (рисунок 1), представляющий собой груз массой m, укрепленный на двух пружинах жесткостью c каждая. Груз находится в трубке, заполненной жидкостью. Сопротивление движению груза может изменяться в зависимости от величины зазора между грузом и стенками трубок и в зависимости от вязкой жидкости. Считать, что сопротивление движению груза прямо пропорционально скорости движения.

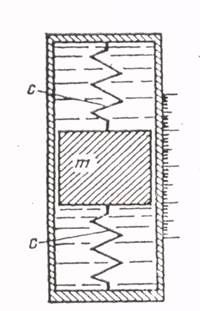
Рисунок 1 – Математическая модель

При движении груза на него действует сила инерции - , сила сопротивления пружин 2сх и сила вязкого сопротивления жидкости . С учетом этих сил дифференциальное  уравнение движения груза представлен в виде

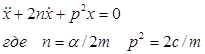
F(t) = F₀sin(wt) – возмущающая сила, действующая на систему. Все параметры функции подобрать самостоятельно.

Выполнение без варьируемого параметра:

На рисунке 2,3 изображено перемещение и скорость соответственно в зависимости от времени

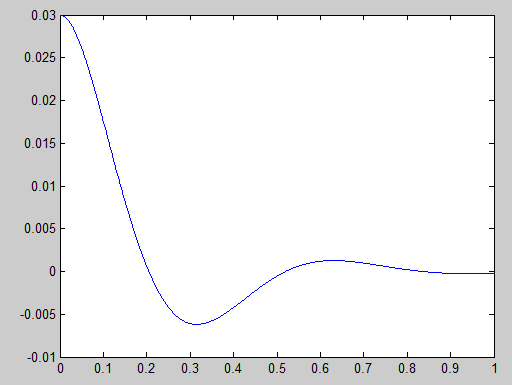
Рисунок 2 – Перемещение

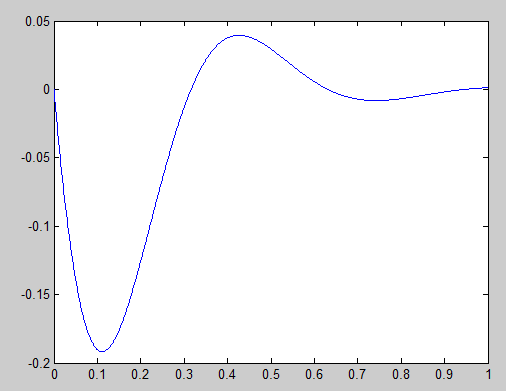
Рисунок 3 -  График скорости

Листинг программ:

Файл Lab5_2.m – функция

function ur2 = Lab5_2(t,x);

%создаем матрицу

ur2=zeros(2,1);

%исходные данные

a=500;

m=50;

c=3100;

n=a/(2*m);

p=(2*c/m)^0.5;

%описание системы  д/у

ur2(1)=x(2);

ur2(2)=-2*n*x(2)-p^2*x(1);

end

Файл Lab5.m – Основная программа

%начальные условия

x0=[0.03 0];

% решение д/у

[T, X]=ode45(@Lab5_2,[0:0.001:1],x0);

%сторим график

figure(1)

plot(T,X(:,1))

figure(2)

plot(T,X(:,2))

Выполнение с варьируемого параметра:

На рисунке 4 график перемещения от варьируемой массы. На рисунке 5 точки минимумов перемещений. На рисунке 6 аппроксимирующая зависимость (полином 3-й степени).

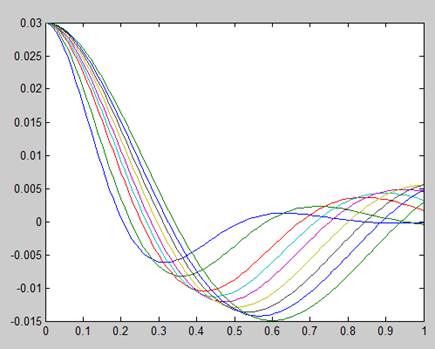
Рисунок 4 – График перемещений от масс

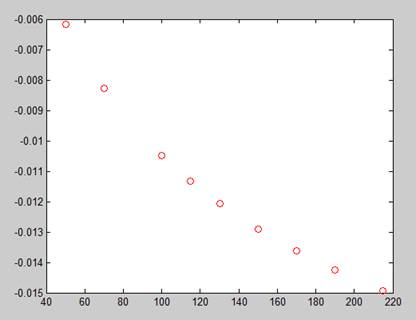
Рисунок 5 – Точки минимума от варьируемой массы

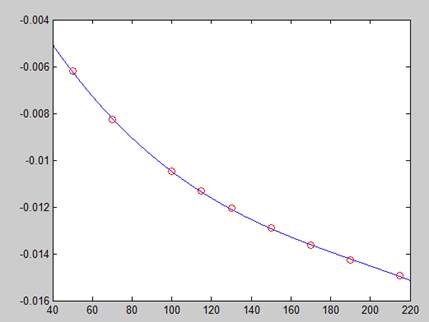
Рисунок 6 – График с аппроксимирующей зависимостью

Файл Lab5_4.m – функция, варьируемый параметр

function ur2 = Lab5_4(t,x,m);

ur2=zeros(2,1);

%исходные данные

a=500;

c=3100;

n=a/(2*m);

p=(2*c/m)^0.5;

%описание системы  д/у

ur2(1)=x(2);

ur2(2)=-2*n*x(2)-p^2*x(1);

end

Файл Lab5_3.m – основная программа  с варьируемым параметром

x0=[0.03 0];

%варьируемый параметр

M=[50 70 100 115 130 150 170 190 215];

for i=1:length(M)

    m=M(i);

    %решение д/у

    diap=0:0.01:1;

    [T, X]=ode45(@Lab5_4,diap,x0, [], m);

    R(:,i)=X(:,1);

end

figure(1)

plot(T,R(:,1:length(M)))

MR=min(R)

figure(2)

plot(M,MR,'or')

p=polyfit(M,MR,3)

z=40:0.001:220;

Z=polyval(p,z);

figure(3)

plot(z,Z,M,MR,'or')

Задание: 2 часть

6. Разработать графический пользовательский интерфейс для реализованной модели (п.1 и п.2).  Обеспечить ввод варьируемого параметра модели с использованием слайдера.

7. Определить время, при котором амплитуда перемещения достигает заданного порогового значения, указанного пользователем; дать графическую интерпретацию полученным результатам.

Результат выполнения:

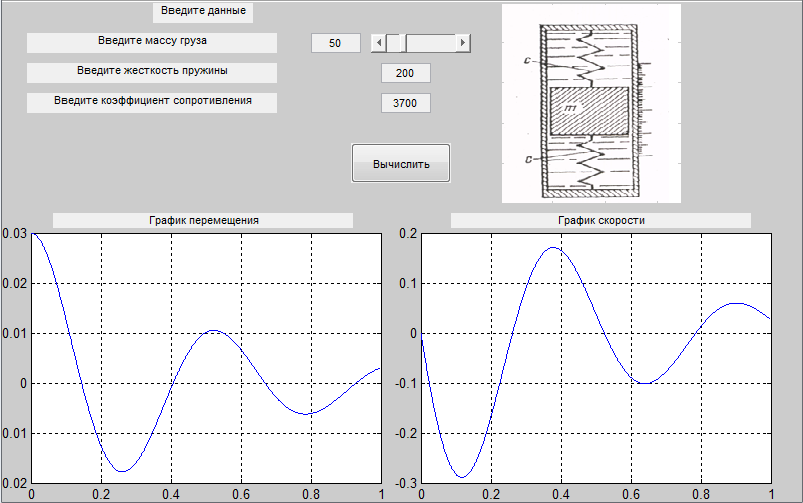
Рисунок 7 - Графический пользовательский интерфейс

Листинг программы файла Lab5_5.m

%очистка экрана

clc

%очистка переменных из памяти

clear all 

%глобальные переменные

global hf ha1 ha2 ha3 he_m he_g he_k hs

%оздание основного окона

hf=figure('units','pixel','Position',[0,0,800,500]);

%Создание окон для графиков двух и рисунков

ha1=axes('units','pixel','Position',[30,20,350,250]);

ha2=axes('units','pixel','Position',[420,20,350,250]);

ha3=axes('units','pixel','Position',[500,300,180,200])  ;

%загружаем рисунок

tx=imread('1.png','png');

image(tx);

col=get(hf,'color');

set(ha3,'XColor',col);

set(ha3,'YColor',col);

%выводим кнопку вычислить

hbt1=uicontrol(hf,'Style','pushbutton','Position',[350,320,100,40],'Callback','Lab5_6','String','Вычислить');

%выводим текст в окно

uicontrol(hf,'style','text','Position',[52,275,300,15],'String','График перемещения');

uicontrol(hf,'style','text','Position',[450,275,300,15],'String','График скорости');

uicontrol(hf,'style','text','Position',[152,480,100,20],'String','Введите данные');

uicontrol(hf,'style','text','Position',[26,450,250,20],'String','Введите массу груза');

uicontrol(hf,'style','text','Position',[26,420,250,20],'String','Введите жесткость пружины');

uicontrol(hf,'style','text','Position',[26,390,250,20],'String','Введите коэффициент сопротивления');

%uicontrol(hf,'style','text','Position',[26,360,250,20],'String','Введите пороговое значение амплитуды');

%uicontrol(hf,'style','text','Position',[26,330,250,20],'String','Значение времени равно: ');

hs=uicontrol(hf,'style','slider','Position',[370,450,100,19],'Max',250,'Callback','Lab5_6')

he_m=uicontrol(hf,'style','edit','Position',[310,450,50,20],'String','0');

he_g=uicontrol(hf,'style','edit','Position',[380,420,50,20],'String','200')  ; 

he_k=uicontrol(hf,'style','edit','Position',[380,390,50,20],'String','3700');

%he_min=uicontrol(hf,'style','edit','Position',[380,360,50,20],'String','0.01') ;

%he_t=uicontrol(hf,'style','edit','Position',[380,330,50,20],'String','')  ;

Листинг программы файла Lab5_6.m

m=get(hs,'Value');                        

set(he_m,'String',num2str(m));             

g=str2num(get(he_g,'string'));           

k=str2num(get(he_k,'string')); 

%min=str2num(get(he_min,'string'));  

x0=[0.03 0]

% решение д/у

[T, X]=ode45(@Lab5_7,[0:0.0009:1],x0,[],m,g,k);

%Определить время, при котором амплитуда перемещения достигает