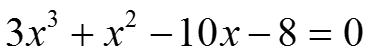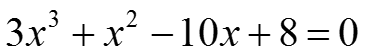Численное интегрирование и решение уравнений и систем в MatLab
18.02.2016
1
План лекции
-
Численное интегрирование
-
Решение уравнений
-
Решение систем уравнений
-
Графическая интерпретация решения уравнений и систем
18.02.2016
2
Численное интегрирование
-
Одной из распространенных задач численного анализа является вычисление определенных интегралов.
-
В MatLab для этой цели используются различные методы, реализованные в следующих стандартных функциях.
18.02.2016
3
Численное интегрирование
-
trapz - вычисление интеграла методом трапеций;
-
quad - вычисление интеграла методом Симпсона;
18.02.2016
4
Численное интегрирование
-
quad8 - вычисление интеграла методом Ньютона-Котеса;
-
dblquad- вычисление интеграла по областям.
18.02.2016
5
Численное интегрирование
-
Подынтегральная функция может быть описана несколькими способами:
-
в обычном виде y=f(x);
-
в форме символьной строки;
-
в виде строкового объекта;
-
с использование М-файла.
18.02.2016
6
-
Функция trapz имеет следующий общий вид:
-
trapz( X, Y),
18.02.2016
7
-
где
-
Х – переменная, указывающая пределы интегрирования (диапазон, вектор);
-
Y – подынтегральная функция.
18.02.2016
8
-
Например, нужно вычислить интеграл функции y= sin(x) в пределах от 1 до 2.
-
>> x=1:0.1:2; y=sin(x);
-
>> trapz(x,y)
-
ans =
-
0.9557
18.02.2016
9
-
Функция quad имеет следующий общий вид:
-
quad( F, A, B, TOL),
-
где
-
F – имя подынтегральной функции f(x);
-
A, B – пределы интегрирования;
-
TOL – абсолютная погрешность вычисления (необязательный параметр)
18.02.2016
10
-
Имя функции может быть задано несколькими способами:
-
выбором из списка простейших функций со знаком @, например, @sin;
-
описанием функции как строки символов;
18.02.2016
11
-
описанием функции как строкового объекта с помощью стандартной функции
-
inline (S),
-
где S – символьное представление функции f(x).
18.02.2016
12
-
>> quad('2*x+sin(x)',0,3)
-
ans =
-
10.9900
-
>>y=inline('2*x+sin(x)');
-
>> quad(y,0,3)
-
ans =
-
10.9900
18.02.2016
13
-
>> quad(@cos,0,3)
-
ans =
-
0.1411
18.02.2016
14
-
Пример 1. Вычислить определенный интеграл методом трапеций и методом Симпсона, сравнить полученные результаты по точности, дать графическую интерпретацию результатов вычислений
18.02.2016
15
%Метод трапеций
x=0:0.01:6;
y=-2*x+sin(x);
z=trapz(x,y)
%Метод Симпсона
18.02.2016
16
y1=inline('-2*x+sin(x)');
z1=quad(y1,0,6)
%Графическое изображение
plot(x,y)
grid on
18.02.2016
17
Решение уравнений
-
Для решения уравнения Y(x)=0, где Y(x) является полиномом, используется стандартная функция roots следующего общего вида:
-
roots(a),
18.02.2016
18
Решение уравнений
-
где
-
а – вектор коэффициентов перед неизвестными полинома размерностью n+1(n – порядок полинома).
-
Результатом работы этой функции будет вектор корней полинома размерностью n.
18.02.2016
19
Решение уравнений
Решение уравнения
>> v=[3 1 -10 -8];
>> roots(v)
ans =
2.0000 -1.3333 -1.0000
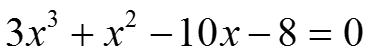
18.02.2016
20
Решение уравнений
Решение уравнения
>> v=[3 1 -10 8];
>> roots(v)
ans =
-2.2936
0.9801 + 0.4495i
0.9801 - 0.4495i
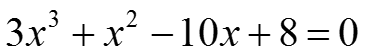
18.02.2016
21
Решение уравнений
Для решения нелинейного уравнения f(x)=0 используется стандартная функция fzero следующего упрощенного общего вида:
18.02.2016
22
Решение уравнений
fzero(f, x0),
где
f – имя функции f(x) исходного уравнения,
х0 – начальное приближение корня.
18.02.2016
23
Решение уравнения
cos(x) – 0.1x=0
>>fzero('cos(x)-0.1*x',1)
ans =
1.4276
18.02.2016
24
Решение уравнения
sin(x)-0.5=0 при х0=2
>> x0=2; y=inline('sin(x)-0.5'); fzero(y,x0)
ans =
2.6180
18.02.2016
25
Решение систем уравнений
-
Для решения систем линейных уравнений в Matlab существует нескольео способов:
-
применение операции левого матричного деления;
-
использование обратной матрицы.
18.02.2016
26
Если задана система линейных алгебраических уравнений вида:
AX=B,
где
18.02.2016
27
А – матрица коэффициентов перед неизвестными системы,
В – вектор свободных членов,
то решение системы может быть найдено в виде:
Х=А \ B
18.02.2016
28
То же самое решение может быть получено с помощью обратной матрицы, например:
X=inv(A)*B
18.02.2016
29
-
Решить систему линейных уравнений 3х+5y=2
-
6x -8y=-3
18.02.2016
30
>>A=[3 5;6 -8]; B=[2 ;-3];
>>X=inv(A)*B
X =
0.0185
0.3889
18.02.2016
31
-
Решить систему линейных уравнений 3a+7b=-13
-
5a +b=1
18.02.2016
32
>> A=[3 7;5 1]; B=[13; 1];
>>X=A\B
X =
-0.1875
1.9375
18.02.2016
33
Графическая интерпретация решения уравнений и систем
-
Для того, чтобы доказать графически, что корни уравнения или системы найдены правильно, нужно:
-
построить график функции левой части уравнения y(x) в диапазоне найденных корней уравнения;
18.02.2016
34
Графическая интерпретация решения уравнений и систем
-
отметить в виде точек корни уравнения;
-
убедиться, что отмеченные точки являются точками пересечения графика функции с осью Х.
18.02.2016
35
Графическая интерпретация решения уравнений и систем
-
Пример 3. Решить уравнение, доказать графически, что корни найдены верно