










МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П.О. СУХОГО
Факультет автоматизированных и информационных систем
Кафедра «Информационные технологии»
ОТЧЁТ О ЛАБОРАТОРНОЙ РАБОТЕ №1
по дисциплине «КМИМ»
на тему: «Освоение интерфейса и выполнение простейших вычислений в системе компьютерной математики MATLAB
»
Выполнила: студентка группы ИТ-32
Принял: преподаватель
Дата сдачи отчёта: __________
Дата допуска к защите: __________
Дата защиты: __________
Гомель 2014
Лабораторная Работа №1
Освоение интерфейса и выполнение простейших вычислений в системе компьютерной математики MATLAB
Цель работы: Освоение интерфейса, управления окнами вывода и режимов работы в системе компьютерной математики MATLAB; освоение вычислений в командном и программном режимах; Освоение методов обработки векторов и матриц в MATLAB; получение навыков решения уравнений и систем; Освоение методов построения графиков в MATLAB; получение навыков форматирования графиков, освоение режима многооконного вывода графиков.
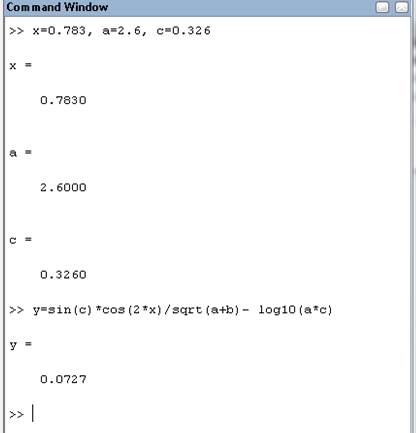
Присвоить значения переменным и вычислить значение арифметического выражения с использованием оператора присваивания в командном режиме:
|
11 |
y = |
x = 0,783 a = 2,6 c = 0,326 |
Результат
2. Создание векторов с использованием диапазона значений переменной
2.1 Создать одномерный массив как диапазон с заданными пределами изменения. Массив должен содержать не менее 10 чисел. Сформировать новый одномерный массив, содержащий значения функции от элементов исходного массива.
|
№ |
Функция |
хн |
хк |
|
11. |
|
1 |
2 |
Решение:
x=1:0.1:2
y=sqrt(x.^2-1)./x
Результат:
y =
Columns 1 through 9
0 0.4166 0.5528 0.6390 0.6999 0.7454 0.7806 0.8087 0.8315
Columns 10 through 11
0.8503 0.8660
2.2 Вычислить множество значений заданных функции, если значения ее аргумента изменяются от a до b с шагом h
|
№ |
Функция 1 |
Функция 2 |
a |
b |
h |
|
11 |
y = sin2(x/3) |
z = 0.01(x2 - 40sin(x)) |
-8 |
8 |
1 |
Решение:
x=-8:1:8
y=sin(x./3).^2
z=0.01*(x.^2-40*sin(x))
Результат:

3 Обработка матриц и векторов
|
11. |
A= |
3.1 Создать вектор V1 из второй строки матрицы А, вектор V2 из третьего столбца матрицы В и вектор V3 из второго столбца матрицы А.
Решение:
A=[6, 9, 4; -9, -1, 1; 10, 1, 7]
B=[1, 1, 1; 3, 4, 3; 0, 5, 2]
v1=A(2, :)
v2=B(:, 3)
v3=A(:, 2)
Результат:

3.2 Вычислить V1×V2, A×V2
Решение:
vv=v1*v2
F=A*v2
Результат:
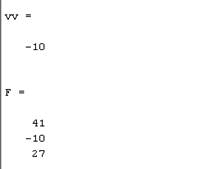
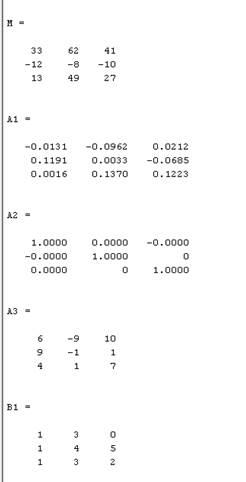
3.3 ВычислитьA×B, A-1, A-1×A, AT, BT
Решение:
M=A*B
A1=inv(A)//инвертированная матрица
A2=inv(A)*A
A3=A.'
B1=B.'//транспонированная матрица
Результат:
3.4 Вычислить определители А и В.
Решение:
detA=det(A)
detB=det(B)
Результат:

3.5 Выполнить поэлементное умножение V3*V2 и A*B
Решение:
V=v3.*v2
AB=A.*B
Результат:
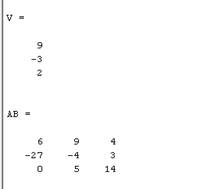
4. Вычисление сумм, произведений
4.1 Вычислить сумму
|
11 |
|
Решение:
i=3:16;
S=sum((-1).^(i+1)./(i-2).^3)
Результат:

4.2 Вычислить произведение
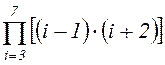
Решение:
i=3:7;
p=prod((i-1).*(i+2))
Результат:

5. Вычисление интегралов различными методами
Вычислить определенный интеграл методом трапеций и методом Симпсона
|
11 |
|
Решение:
x=0.1:0.01:4.2;
y=1./(x.^2+3*x);
z1=trapz(x, y)
z2=quad('1./(x.^2+3*x)', 0.1, 4.2)
Результат:

6. Решение уравнений и систем алгебраических уравнений
6.1 Найти корень уравнения с применением функции fzero, используя заданное начальное значение.
|
11. |
|
|
Решение:
fzero('sqrt(x^2-x-1)+sqrt(x^2+x+3)-sqrt(2*x^2+8)', 5)// Для решения нелинейного уравнения
Результат:
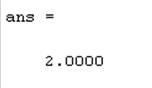
6.2 Вычислить множество корней уравнения с использованием функции roots
11. ![]()
Решение:
v=[1 -12.8 2.15 -2.8 1.15];
roots(v)// Для решения полинома
Результат:

6.3 Решить систему линейных уравнений матричным методом
|
11. |
|
Решение:
A=[2 -1 2;4 1 4;1 1 2];
B=[0;6;4];
X=inv(A)*B//решение с помощью обратной матрицы
Y=A\B// левое матричное деление
Результат:

7. Графики
7.1 Построить график функции в заданных пределах изменения ее аргумента
|
№ вар. |
Функция |
|
|
|
11. |
|
1 |
4 |
Решение:
X=1:0.01:4
Z= exp(X).*(sin(3*X)-3*cos(3*X))
plot(X,Z)//строим график
Результат:
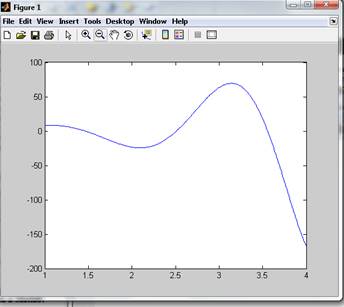
7.2 Построить на одном поле графики двух функций, промаркировать точки графиков, задать типы линий, подписать оси и весь график, создать легенду, нанести координатную сетку, нанести на график произвольный текст
|
№ вар. |
Функция |
|
|
№ вар. |
Функция |
|
|
|
11. |
|
1 |
4 |
12. |
|
1 |
4 |
Решение:
figure(2)
X=1:0.01:4
Z1= exp(X).*(sin(3*X)-3*cos(3*X));
Z2=(X.^2-2*X)
plot(X,Z1,'--om',X,Z2,'-og')//строи 2 графика: 1-пунктироной линией с кругами фиолетового цвета; 2-сплошной линией с кругами зеленого цвета
grid();//добавляем сетку
title(' Grafic:');//подписываем график
xlabel('X');//подписываем ось х
ylabel('Z');//подписываем ось у
legend('Z1','Z2');//подписываем линии
Результат:
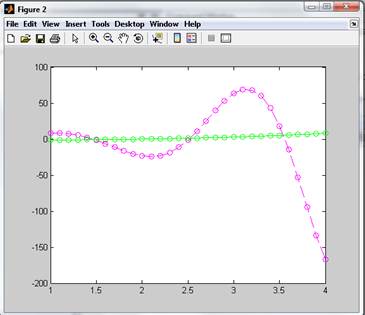
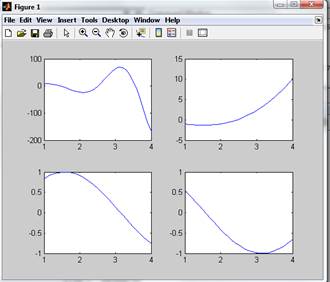
7.3 Разбить графическое окно на 4 области, в которых построить графики п.1, 2 и графики функций y=sin(x) и y=cos(x)
Решение:
subplot(2, 2, 1) //разбиение файла на 4 области и построения графика в первой
X=1:0.0:4
Z1= exp(X).*(sin(3*X)-3*cos(3*X))
plot(X,Z1)//строим график
subplot(2, 2, 2)
X=1:0.0:4
Z2=(X.^2-2*X).*log(X)-1,5*X.^2+4*X
plot(X,Z2)
subplot(2, 2, 3)
X=1:0.0:4
Z3=sin(X)
plot(X,Z3)
subplot(2, 2, 4)
X=1:0.0:4
Z4=cos(X)
plot(X,Z4)
Результат:
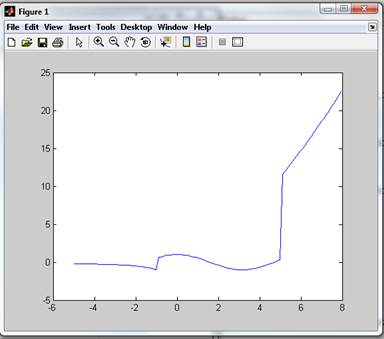
7.4 Построить график кусочно-непрерывной функции. Пределы изменения аргумента подобрать так, чтобы перекрывались все три диапазона. При задании вида функции необходимо использовать программный фрагмент, нанести координатную сетку, оцифровать оси, задать легенду для каждой линии графика, сделать надписи по осям и заголовок графика, изменить тип, цвет, толщину линии графика, нанести маркеры на линии графика.
|
№ |
Вид функции |
|
11 |
|
Решение:
xn=-5
xk=8;
dx=0.1;
x=xn;
i=0;
while x<=xk
if x>5, y=sqrt(x.^3);
else if (x>=-10) & (x<=-1), y=1./x;
else y=cos(x);
end
end
i=i+1;
X(i)=x;
Y(i)=y;
x=x+dx;
end
plot(X, Y);
Результат:
Выводы: Рассмотрели интерфейс, управления окнами вывода и режимов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.