МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П.О. СУХОГО
Факультет автоматизированных и информационных систем
Кафедра «Информационные технологии»
ОТЧЁТ О ЛАБОРАТОРНОЙ РАБОТЕ №3
по дисциплине «КМИМ»
Выполнила: студент группы ИТ-32
Принял: доцент
Дата сдачи отчёта: __________
Дата допуска к защите: __________
Дата защиты: __________
Гомель 2015
Часть 1. Обработка результатов натурного эксперимента, синтез модели (2 часа)
1) Создать с использованием программы «Блокнот» файл значений функции, полученной в результате эксперимента. Считать файл в вектор Y. Вектор аргумента функции X создать с использованием формулы, приведенной в задании. Построить график полученной функции Y(X).
2) Выполнить сплайновую интерполяцию исходной функции. Сделать графическую интерпретацию результатов.
3) Выполнить табулирование интерполирующей функции. Записать полученный вектор в файл на диске.
Описание математической модели
В результате эксперимента был получен вектор данных размерностью 2N+1, который размещен в текстовом файле.
Известно, что значения независимого параметра x можно рассчитать аналитически:
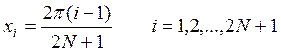
Необходимо рассчитать значения экспериментальной зависимости не менее, чем в 100 точках и записать полученные данные в файл для дальнейшей обработки модели.
|
№ |
Значения функции Y |
|
9 |
1.1; 2.4; 5.4; 10.4; 16.3; 19.9; 18.6; 13.4; 7.7; 3.6; 1.6; 0.64; 0.27; 0.13; 0.7; 0.5; 0.588; 0.6; 0.9; 0.18; 0.4 |
Решение:
Y=load('input.dat');
i=1:1:length(Y);
X=2*3.14*(i-1)/length(Y);
%интерполирует значения функции Y в точках xi внутри области определения функции, используя кубические сплайны
xi=0:0.001:6;
yi=spline(X,Y,xi);
%вычислим коэффициенты аппроксимирующего полинома степени 18(вычисляет методом наименьших квадратов)
p=polyfit(X,Y,18);
%вычислим значения полинома в точках сетки
f=polyval(p,xi);
figure(1);
plot(X, Y, 'o', xi, yi, 'g');
figure(2);
plot(X, Y, 'o', xi, f);
%сохранение вектора табулирования интерполирующей функции
save('danY.txt','f','-ascii')
Результат:
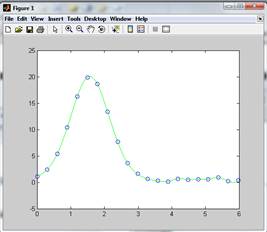
Рисунок 1.1 - Сплайновая интерполяция исходной функции
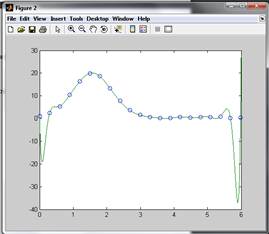
Рисунок 1.2 – график табулирования интерполирующей функции
1. Считать с диска заданный файл исходных данных, сформировать вектор временного интервала, построить график функции ЭДС в зависимости от времени.
2. Выполнить сглаживание экспериментальных данных с помощью различных функций аппроксимации. Сравнить полученные результаты, дав им графическую интерпретацию.
3. Выделить участок исходной функции от максимального до минимального значений, аппроксимировать его с помощью линейной регрессии, функцию для аппроксимации подобрать самостоятельно.
Задан файл результатов эксперимента в числовом виде, задано время проведения эксперимента.
|
N варианта |
Имя файла |
Время исследований |
|
1 |
tan1.dat |
0.01 |
Описание предметной области
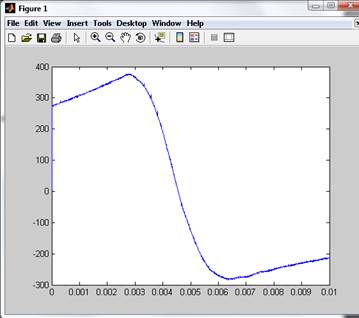
Для исследования свойств металлов используется магнитоиндукционная установка, электрическая часть которой представляет собой систему аналого-цифрового преобразования сигнала индукционного датчика. Типичная кривая изменения ЭДС, снимаемая с установки, имеет вид, приведенный на рисунке.
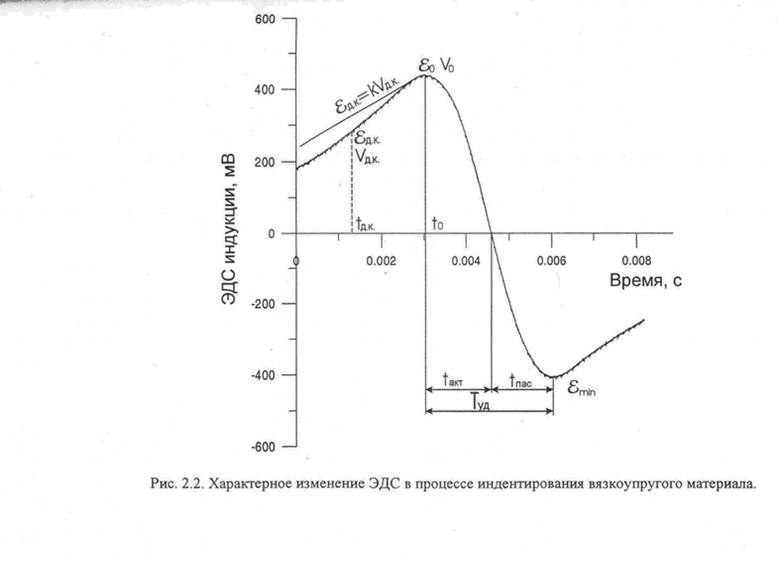
Результирующие значения ЕДС записаны в файл. Основной задачей исследования является подбор аппроксимирующей сглаживающей зависимости за весь период наблюдения, а особенно на участке перехода от максимального значения ЕДС до минимального.
Решение:
%Считываем с диска заданный файл исходных данных, формируем вектор
%временного интервала, строим график функции ЭДС в зависимости от времени.
h = 0.01/(length(Y)-1);
t = 0:h:0.01;
figure(1)
plot(t,Y)
maxY = Y(1);
minY = Y(1);
for i=1:length(Y)
if Y(i)>maxY;
maxY = Y(i);
imax = i;
end
end
for i=1:length(Y)
if Y(i)<minY;
minY = Y(i);
imin = i;
end
end
j=1;
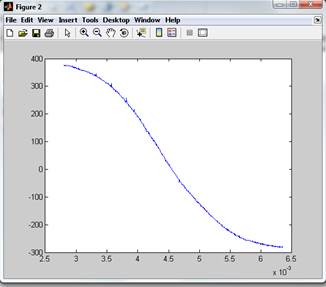
%Выделяем участок исходной функции от максимального до минимального
%значений
for i = imax:imin
Y1(j) = Y(i);
t1(j) = t(i);
j = j+1;
end
figure(2)
plot(t1,Y1)
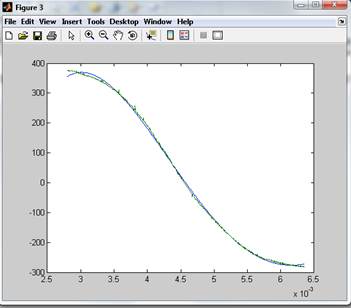
p = polyfit(t1,Y1,4);
f = polyval(p,t1);
figure(3)
plot(t1,f,t1,Y1)
Результат:
Часть 2. Обработка результатов эксперимента по компьютерной модели (2 часа)
Постановка задачи
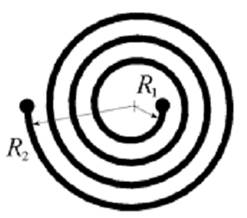
В интегральных схемах используются плоские катушки индуктивности в виде круглой металлической спирали. Индуктивность такой катушки (в наногенри) приближенно определяется по формуле
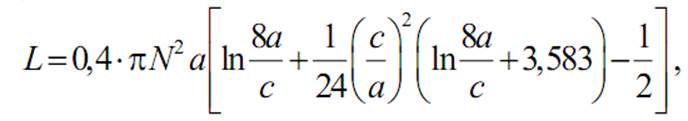
где π = 3,14…,
N − число витков,
a = (R1 + R2) / 2,
с = R2 – R1,
R1 и R2 − внутренний и внешний радиусы.
Все размеры в формулах указаны в миллиметрах.
Задание
1) Найдите радиус R2, удовлетворяющий требуемому значению индуктивности L при указанных в таблице N и R1. Доказать графически, что значение R2 найдено верно.

Решение:
R1=1.5; %внутренний радиус
N=6; %число витков
L=250; %индуктивность
%функция, определяющая значения внешнего радиуса
Fz1=@(R2)(0.4*pi*N^2*(R1+R2)/2.*(log(8*(R1+R2)/2./(R2-R1))+1/24*((R2-R1)./(R1+R2)/2).^2.*(log(8*(R1+R2)/2./(R2-R1))+3.583)-1/2)-L);
Rk=fzero(Fz1,5);%поиск корней
Rp=6:0.001:7;%формируем вектор промежуток значений внешнего радиуса подстовляемый в функцию
y=Fz1(Rp);%получаем значение фнукции
%Выводим значение радиуса R2
disp('R2=');
disp(Rk);
%Строим график
figure(1);
plot(Rp,y,Rk,-10:10,'.-r');
xlabel('6\leq Rp \leq 7');
ylabel('y');
title('Grafic Fz1(R2)');
grid;%подключаем сетку
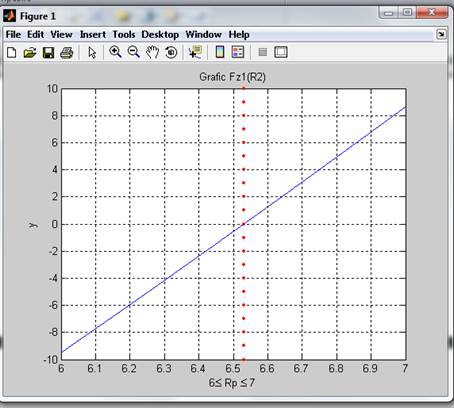
Результат:
R2=
6.5311
2) Рассчитать значение радиуса R2 для 6 -7 значений из диапазона значений варьируемого параметра, указанного в таблице. Построить сводный график зависимости полученных значений радиуса R2 от варьируемого параметра.
|
Вариант |
R1 |
|
6-1 |
1 – 2 |
Решение:
%Исходные данные
N=6; %число витков
L=250; %индуктивность
R1=1:0.01:2;
Rp=2:0.01:10;%формируем вектор промежуток значений внешнего радиуса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.