Построение и исследование явных аналитических моделей. Постановка задачи моделирования

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО

Факультет автоматизированных и информационных систем

Кафедра «Информационные технологии»

ОТЧЕТ   ПО   ЛАБОРАТОРНОЙ   РАБОТЕ   № 2

по дисциплине «Компьютерные методы инженерного моделирования»

Выполнила:  студентка гр. ИТ-31

Е

Принял:        преподаватель

Гомель 2014

ЛАБОРАТОРНАЯ РАБОТА №2

Построение и исследование явных аналитических моделей

Цель работы: Получить навыки компьютерного моделирования технических объектов, представленных в виде явной аналитической модели с выводом результатов моделирования в численном и графическом виде.

Задача 1

Постановка задачи моделирования

1) Разработать компьютерную модель манипулятора, которая имеет следующие выходные параметры:

− значения угла поворота звена ОА в зависимости от времени;

− значения координат шарнира А и захвата С в зависимости от времени.

Результаты моделирования представить в численном и графическом виде.

2) Исследовать модель, для чего определить:

−   максимальное значение координаты Y захвата манипулятора;

− значение координаты X, при котором координата Y захвата манипулятора максимальна.

Исходными данными для построения модели являются: АВ – длина звена АВ; АС – длина звена АС; ОА – длина звена ОА; вид функции закона движения ползуна, заданный аналитически; вид функции закона движения руки АС, заданный аналитически; T_k – конечное значение времени для исследования модели манипулятора.

Описание математической модели

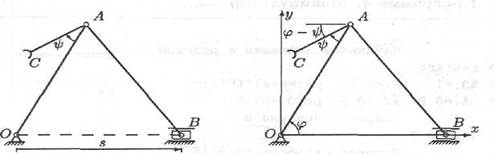
Рисунок 1 – Схема манипулятора

Механизм манипулятора (рисунок 1.1) приводится в движение двумя независимыми приводами. Задан закон движения ползуна:

S1(t) = S0 - Vb∙t

Закон движения руки АС относительно кривошипа ОА имеет вид:

Ψ(t) = Ψ0 + ω∙t

Координаты шарнира А вычисляются по формулам:

XA = OA∙ cos φ      YA = OA∙ sin φ, где угол φ в зависимости от времени вычисляется по формуле:

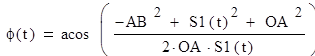
Координаты захвата вычисляются по формулам:

XC = XA - AC∙cos(φ – ψ)     YC = YA - AC∙sin(φ – ψ)

Результат выполнения

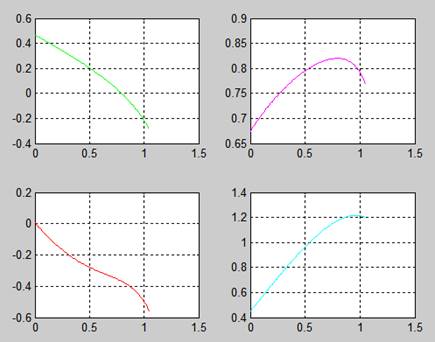
Рисунок 2 – Координаты шарнира и захвата (XA, YA, XC, YC)

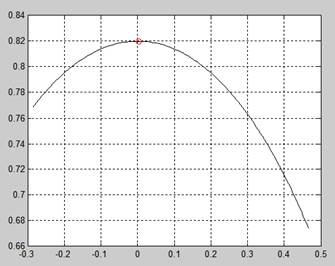
Рисунок 3 – Траектория движения точки A

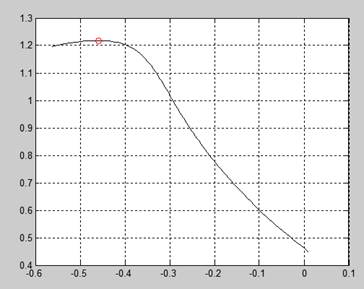
Рисунок 4 – Траектория движения точки С

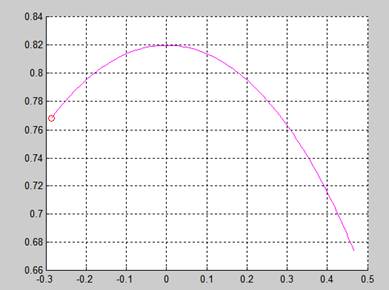
Рисунок 5 – Траектория точки A и сама движущаяся точка

Xmax для рисунка 3 -  0.002991676622859

Ymax для рисунка 3 -  0.819994542586098

Xmax для рисунка 4 -  -0.459409391717378

Xmax для рисунка 4 -  1.218162713654070

Задача 2

Постановка задачи моделирования

1) Разработать компьютерную модель кулачкового механизма, которая имеет следующие выходные параметры:

– функцию аналога ускорения толкателя в зависимости от времени;

– параметры закона движения кулачкового механизма.

2) Исследовать модель, для чего определить следующие параметры:

– максимальные и минимальные значения аналога ускорения кулачкового механизма;

– значение времени, при котором аналог ускорения  кулачкового механизма максимален.

Описание математической модели

Дан кулачковый механизм, закон изменения аналога, ускорения толкателя которого приведен на рисунке 6.

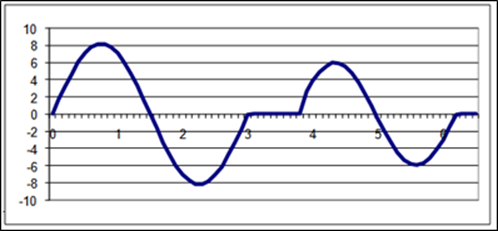
Рисунок 6 – Закон изменения аналога ускорения толкателя

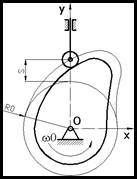
Рисунок 7 – Кулачковый механизм

Функция аналога ускорения толкателя механизма имеет вид:

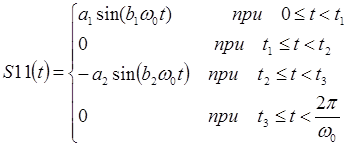
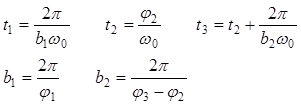
Листинг M-файла

% ЗАДАЧА 1

%исходные данные

%Исходными данными для построения модели являются:

%- АВ – длина звена АВ;

%- АС – длина звена АС;

%- ОА – длина звена ОА;

%- вид функции закона движения ползуна, заданный аналитически;

% - вид функции закона движения руки АС, заданный аналитически;

%- Tk – конечное значение времени для исследования модели манипулятора.

AB=0.96, OA=0.82, AC=0.51, TK=1.05, S0=1.15,Vb=0.82,Y0=0.51,w=2.3;

t=0:0.01:1.05

%закон движения ползуна

S1=S0-Vb*t

%Закон движения руки АС относительно кривошипа ОА имеет вид

psi=Y0+w*t

%уго л фи вв зависимости от времени

fi=acos((-AB^2+S1.^2+OA^2)./(2*OA*S1))

%Координаты шарнира А вычисляются по формулам

XA=OA*cos(fi)

YA=OA*sin(fi)

%Координаты захвата вычисляются по формулам

XC=XA-AC*cos(fi-psi)

YC=YA-AC*sin(fi-psi)

figure(1)

subplot(2, 2, 1)

plot(t,XA,'-g')

grid on

subplot(2, 2, 2)

plot(t,YA,'-m')

grid on

subplot(2, 2, 3)

plot(t,XC,'-r')

grid on

subplot(2, 2, 4)

plot(t,YC,'-c')

grid on

n=1;

Ymax=YA(1);

for i=1:length(YA)

if(YA(i)>Ymax)

Ymax=YA(i)

n=i;

end

end

Xmax=XA(n);

nn=1;

Ycmax=YC(1);

for i=1:length(YC)

if(YC(i)>Ycmax)

Ycmax=YC(i)

nn=i;

end

end

Xcmax=XC(nn);

figure(2)

plot(XA,YA,'--g',Xmax, Ymax, 'or')

figure(3)

plot(XC,YC,'--g',Xcmax, Ycmax, 'or' )

figure(4)

hold on

plot(XA,YA,'-m')

ph1=plot(XA(1),YA(1),'or')

for i=1:numel(XA)

set(ph1,'XData',XA(i),'YData',YA(i))

pause(0.04)

end

% ЗАДАЧА 2

%исходные данные

fi1=1.63, fi2=2.14, fi3=4.92, a1=9.5, a2=4.0, amega0=1.256

pi=3.14

b1=2*pi/fi1;

b2=2*pi/(fi3-fi2);

t1=2*pi/(b1*amega0);

t2=fi2/amega0;

t3=t2+(2*pi/(b2*amega0));

t_kon=2*pi/amega0;

t=0:0.01:t_kon;

for i=1:1:numel(t)

if (t(i)>=0) && (t(i)<t1)

s11(i)=a1*sin(b1*amega0*t(i))

else

if(t(i)>=t1)&&(t(i)<t2)

s11(i)=0

else

if(t(i)>=t2)&&(t(i)<t3)

s11(i)=-a2.*sin(b2.*amega0.*t(i))

else

s11(i)=0

end

end

end

i=i+1;

end

hold on

Ymax=s11(1)

n=1;

for i=1:numel(s11)

if s11(i)> Ymax

Ymax = s11(i);

n=i;

end

end

Xmax = t(n);

Ymin=s11(1)

n=1;

for i=1:numel(s11)

if s11(i)< Ymin

Ymin = s11(i);

n=i;

end

end

Xmin = t(n);

figure(1);

plot(t,s11,Xmax,Ymax,'or');

plot(t,s11,Xmin,Ymin,'or');

grid on

Результаты выполнения

Значения Xmax= 0.819994542586098, Ymax= 9.497639086251352, Xmin= 0.970000000000000, Ymin= -9.498375497415026

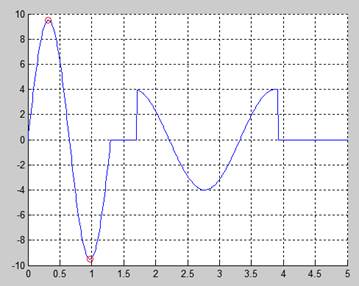
Рисунок 8 – Закон изменение аналога

Вывод: Получила навыки компьютерного моделирования технических объектов, представленных в виде явной аналитической модели с выводом результатов моделирования в численном и графическом виде.