Интерференция света при отражении от тонких плёнок. Плоскопараллельная пластинка и полосы равного наклона

1

Лекция№ 5

Темалекции:

Интерференциясвета(продолжение)

Рассматриваемыевопросы:

1.  Интерференция света при отражении от тонких плёнок…………….……….1

2.  Плоскопараллельная пластинка  и полосы равного наклона.….…………….4

3.  Пластинка переменной толщины и полосы равной толщины….………..…10

4.  Кольца Ньютона……………………………………………………………….15 5. Интерферометр Майкельсона…………………………….…………………..18

       6.       Многолучевая интерференция. Интерферометр Фабри – Перо.………...…22

1. ИНТЕРФЕРЕНЦИЯ СВЕТА ПРИ ОТРАЖЕНИИ ОТ ТОНКИХ ПЛЁНОК

При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при известных условиях могут интерферировать, рис. 1.

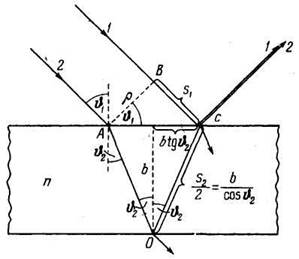
Рис. 1.

2

Пусть на прозрачную плоскопараллельную пластинку (рис. 1) падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отбрасывает вверх два параллельных пучка света, из которых один образовался за счет отражения от верхней поверхности пластинки, второй — вследствие отражения от нижней поверхности (на рис. 1 каждый из этих пучков представлен только одним лучом). При входе в пластинку и при выходе из нее второй пучок претерпевает преломление. Кроме этих двух пучков, пластинка отбросит вверх пучки, возникающие в результате трех-, пяти- и т. д. кратного отражения от поверхностей пластинки. Однако ввиду их малой интенсивности мы эти пучки принимать во внимание не будем. Не будем также интересоваться пучками, прошедшими через пластинку.

Разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке  С, равна

                             (1) где s₁ — длина отрезка ВС, a s₂ — суммарная длина отрезков АОи ОС, п— показатель преломления пластинки. Показатель преломления среды, окружающей пластинку, полагаем равным единице. 

Из рис. 1 (b — толщина пластинки), видно, что  s₁ = 2btgϑ₂ sinϑ₁,

s₂ = 2bcosϑ₂ .

Подстановка этих значений в выражение (1) дает

3

Произведя замену nsin ϑ₂ = sin ϑ₁ и учтя, что

легко привести формулу для ∆ к виду

                     (2)

При вычислении разности фаз о между колебаниями в лучах 1 и 2 нужно, кроме оптической разности хода ∆, учесть возможность изменения фазы волны при отражении. В точке С (см. рис. 1) отражение происходит от границы раздела среды, оптически менее плотной, со средой, оптически более плотной. Поэтому фаза волны претерпевает изменение на π. В точке Оотражение происходит от границы раздела среды оптически более плотной со средой оптически менее плотной, так что скачка фазы не происходит. В итоге между лучами 1 и 2 возникает дополнительная разность фаз, равная π. Её можно учесть, добавив к ∆ (или вычтя из неё) половину длины волны в вакууме. В результате получим

                    (3)

Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой (3). Выясним условия, при которых эти волны окажутся когерентными и смогут интерферировать. Рассмотрим два случая.

4

 2. ПЛОСКОПАРАЛЛЕЛЬНАЯ ПЛАСТИНКА И ПОЛОСЫ РАВНОГО НАКЛОНА

Обе плоские отраженные волны распространяются в одном направлении, образующем с нормалью к пластинке угол, равный углу падения ϑ₁. Эти волны смогутинтерферировать, если будут соблюдены условия как временной, так и пространственной когерентности.

Для того чтобы имела место временная когерентность, разность хода            (3) не должна превышать длину когерентности (предыдущую лекцию), равную

λ² ∆λ≈λ₀(∆λ λ₀)⁻¹

Следовательно, должно соблюдаться условие или

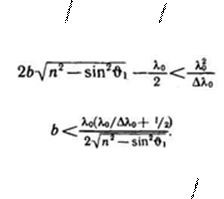
 В полученном соотношении половиной можно пренебречь по сравнению с λ₀ ∆λ₀ . Выражение n² −sin²ϑ₁ имеет величину порядка единицы. Поэтому можно написать

                                (4)

(удвоенная толщина пластинки должна быть меньше длины когерентности).

Таким образом, отраженные волны будут когерентными только в том случае, если толщина

5

пластинки b не превышает величины, определяемой

                                                                                    0                                          0

соотношением (4). Положив λ₀ = 5000 Aи ∆λ₀ = 20 A , получим предельное значение толщины, равное

                   (5)

Теперь рассмотрим условия соблюдения пространственной когерентности. Поставим на пути отраженных пучков экран Э(рис. 2). 

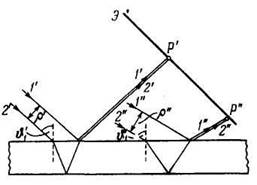
Рис. 2.

Приходящие в точку Р' лучи 1' и 2' отстоят в падающем пучке на расстояние ρ′. Если это расстояние не превышает радиуса когерентности ρ_ког падающей волны, лучи 1' и 2' будут когерентными и создадут в точке Р' освещенность, определяемую значением разности хода ∆, отвечающим углу паденияϑ′₁. 

Другие пары лучей, идущие под тем же углом ϑ′₁, создадут в остальных точках экрана такую же освещенность. 

Таким образом, экран окажется равномерно освещенным.

6

В частном случае, когда

∆ = (m + ¹ )λ₀ ,

2

экран будет темным. 

При изменении наклона пучка (т. е. при изменении угла ϑ₁) освещенность экрана будет меняться.

Из рис. 1 видно, что расстояние между падающими лучами 1 и 2 равно

              (6) Если принять п= 1,5, то для ϑ₁= 45° получается ρ = 0,86b, а для ϑ₁= 10° — ρ = 0,1b . Для нормального падения (ϑ₁= 0) ρ = 0при любом п.

Радиус когерентности солнечного света имеет значение порядка 0,05 мм (см. предыдущую лекцию). При угле падения в 45° можно положить ρ ≈b. Следовательно, для возникновения интерференции в этих условиях должно выполняться соотношение

                               (7)

Для угла падения порядка 10⁰ пространственная когерентность будет сохраняться при толщине пластинки не более 0,5 мм.

Таким образом, вследствие ограничений, накладываемых временной и пространственной когерентностью, интерференция при освещении пластинки солнечным светом будет наблюдаться только