Основы геометрической оптики. Законы геометрической оптики. Преломление одной сферической поверхности

1

Лекция№ 2

Темалекции:

Основыгеометрическойоптики

Рассматриваемыевопросы:

1.  Законы геометрической оптики……………………...…………………………1

2.  Принцип Ферма………………………………………….. ……………………..3

3.  Таутохронные лучи……………………………………………...………………7 

4.  Преломление одной сферической поверхности…...…………………………..9

5.  Тонкая линза…………………………………………………………………....14 

6.  Сферическое зеркало…………………..……………………………………….19

1.  ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ  ОПТИКИ

Длины воспринимаемых глазом световых волн очень малы (порядка 10^-7 м). Поэтому, как упоминалось в предыдущей лекции, распространение видимого света можно в первом приближении рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых линий, называемых лучами.  В предельном случае, соответствующем λ→ 0 , законы оптики можно сформулировать на языке геометрии. В соответствии с этим раздел оптики, в котором пренебрегают конечностью длин волн, называется   геометрической оптикой. Другое название этого раздела — лучевая оптика.

Основу геометрической оптики образуют четыре закона: 

1)  закон прямолинейного распространения света;

2)  закон независимости световых лучей; 3) закон отражения света;

4) закон преломления света.

2

Законпрямолинейногораспространенияутверждает, чтов однородной среде свет распространяется прямолинейно_. 

Этот закон является приближенным: при прохождении света через очень малые отверстия наблюдаются отклонения от прямолинейности, тем большие, чем меньше отверстие.

Законнезависимостисветовыхлучейутверждает, чтолучи при пересечении не возмущают друг друга_.

Пересечения лучей не мешают каждому из них распространяться независимо друг от друга. Этот закон справедлив лишь при не слишком больших интенсивностях света. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей перестает соблюдаться.

Законотражения – отраженныйлучлежитвплоскостипадения, причёмуголотраженияравенуглупадения (i′ = i).

Законпреломления  (ЗаконСнеллиуса) – преломлённыйлучлежитвплоскостипадения, ауголпреломлениясвязансугломпадениясоотношением:

                                               sini     n_r

= = n_ri ,                                      (1) sin r n_i

где i  –  угол падения, r  – угол преломления (рефракции), n_r – показатель преломления в среде распространения преломлённого луча, n_r – показатель преломления в среде распространения падающего луча; n_ri – относительный показатель преломления сред.

3

2. ПРИНЦИП ФЕРМА

В основу геометрической оптики может быть положен принцип, установленный французским математиком Ферма в середине XVII столетия. Из этого принципа вытекают законы прямолинейного распространения, отражения и преломления света.

В формулировке самого Ферма принцип гласит, чтосвет распространяется по такому пути_, для прохождения которого ему требуется минимальное время_.

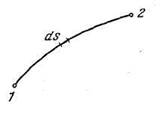
Рис. 1.

Для прохождения участка пути ds (рис. 1) свету требуется время dt = ds/v, где v — скорость света в данной точке среды. Заменив v через cn , где с – скорость света, n – показатель преломления, получим, что 

1

dt = ⋅nds . c

Следовательно, время τ, затрачиваемое светом на прохождение пути от точки 1 до точки 2, равно

nds .                                  (2) c ₁

      Имеющая размерность длины величина

4

L nds .                                  (3) называется оптическойдлинойпути.

В однородной среде оптическая длина пути равна произведению геометрической длины пути s на показатель преломления среды n :

L = ns.                                  (4)

Согласно (2) и (3):

τ= Lc .                                  (5)

Пропорциональность времени прохождения τ оптической длине пути L дает возможность сформулировать принцип Ферма следующим образом: свет распространяется по такому пути_, оптическая длина которого минимальна_. 

Точнее, оптическая длина пути должна быть экстремальной, т. е. либо минимальной, либо максимальной, либо стационарной — одинаковой для всех возможных путей. В последнем случае все пути света между двумя точками оказываются таутохронными (требующими для своего прохождения одинакового времени).

Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален в случае распространения света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении.

                      Получим с помощью принципа Ферма закон

5

отражения света.

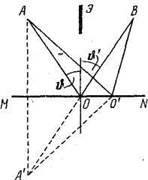
Рис. 2.

Пусть свет попадает из точки Ав точ~ ку В, отразившись от поверхности MN

(рис. 2; прямой путь из А в В прегражден непрозрачным экраном Э). Среда, в которой проходит луч, однородна. Поэтому минимальность оптической длины пути сводится к минимальности его геометрической длины. 

Геометрическая длина произвольно взятого пути равна

АО'В= А'О'В (вспомогательная точка А' является зеркальным изображением точки А₁. Из рисунка видно, что наименьшей длиной обладает путь луча, отразившегося в точке О, для которой угол отражения равен углу падения.

Заметим, что при удалении точки О' от точки Огеометрическая длина пути неограниченно возрастает, так что в данном случае имеется только один экстремум — минимум.

Получим с помощью принципа Ферма закон

6

преломления света, рис. 3.

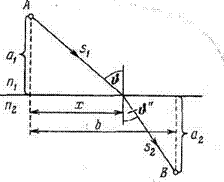
Рис. 3.

Для произвольного луча оптическая длина пути равна

Чтобы найти экстремальное значение, продифференцируем L похи приравняем производную нулю:

Множители при n ₁ и п₂равны соответственно sinϑ и sinϑ′′. Таким образом, получается соотношение

выражающее  закон преломления.

7

3.  ТАУТОХРОННЫЕ ЛУЧИ

Рассмотрим отражение от внутренней поверхности эллипсоида, рис. 4.

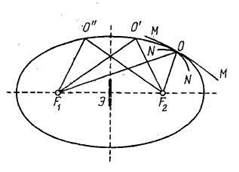
Рис. 4.

Здесь F ₁ и F₂— фокусы эллипсоида. В соответвии с опделением эллипса пути F₁OF₂, F₁O′F₂, F₁O′′F₂ и т. д. одинаковы по длине. Поэтому все лучи, вышедшие из фокуса F₁ и пришедшие после отражения в фокус F₂, являются таутохронными. В этом случае оптическая длина пути стационарна. 

Если заменить поверхность эллипсоида поверхностью ММ, имеющей меньшую кривизну и ориентированной так, рис. 4, что луч, вышедший из точки F₁, после отражения от ММпопадает в точку F₂, то путь F₁OF₂ будет минимальным. 

Для поверхности NN, рис. 4, имеющей кривизну большую, чем у эллипсоида, путь F₁OF₂ будет максимальным.

8

Стационарность оптических путей имеет место также при прохождении лучей через линзу, рис. 5.

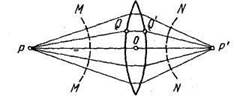
Рис. 5

Луч POP' имеет самый короткий путь в воздухе (где показатель преломления ппрактически равен единице) и самый длинный путь в стекле n ≈1,5. Луч PQQ'P' имеет более длинный путь в воздухе, но зато более короткий путь в стекле. В итоге оптические длины путей для всех лучей оказываются одинаковыми. Поэтому лучи таутохронны, а оптическая длина пути стационарна.

Равенство оптических длин означает равенство времён прохождения светом соответствующих путей