Министерство образования РФ
Рязанская государственная радиотехническая академия
Кафедра ОиЭФ
Лабораторная работа № 1-5
«ИССЛЕДОВАНИЕ ПРЕЦЕССИИ СВОБОДНОГО ГИРОСКОПА»
Цель работы: изучение устройства и движения гироскопа под действием момента внешних сил; определение частоты оборотов ротора и момента сил трения в его подшипниках.
Приборы и принадлежности: гироскоп кардановый подвес, набор сменных грузов, секундомер, стробоскоп частотомер.
Гироскоп это – симметричное быстро вращающееся твёрдое
тел, ось которого может изменять своё положение в пространстве. Для того, что
бы гироскоп свободно мог изменять положение своей оси в пространстве, его
закрепляют на кардановом подвесе. Подобный способ крепления гироскопа
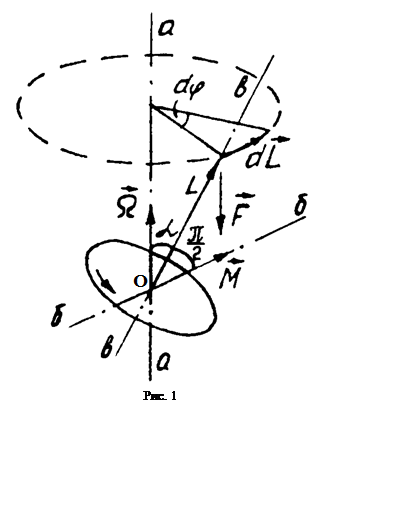
схематично изображен с помощью векторной схемы на рис.1. Где аа –
вертикальная ось вращения; бб – горизонтальная ось вращения; вв –
ось вращения самого гироскопа; O – центр масс гироскопа. Из рисунка видно, что
при повороте вокруг любой оси гироскоп сохраняет своё положение в пространстве
(т.к. в точке все три оси вращения пересекаются в точке O).
Такой гироскоп называется свободным.
Движение гироскопа описывается уравнением:
1)
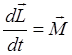, где 
- момент импульса
гироскопа относительно точки пересечения осей; 
- момент внешних сил относительно точки O.
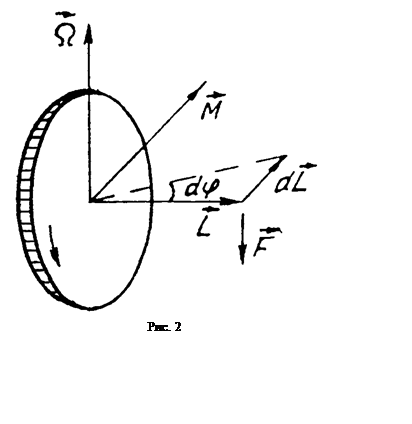
Дальнейшие выводы будут делаться непосредственно с использованием векторной схемы приведённой на рис.1.
Пусть дано: M =
0, а w0 - угловая скорость вращения гироскопа. Тогда L £ J0w0 = const, где
J0 – момент инерции гироскопа относительно оси
вращения вв. Теперь если к оси гироскопа приложить внешнюю силу 
, то возникнет момент
силы , лежащий в
горизонтальной плоскости. Из выражения (1) следует, что векторы и ортогональны. За
промежуток времени dt вектор получает приращение 
, направленное так же,
как и вектор , поэтому сила заставляет описывать
гироскоп окружность в горизонтальной плоскости, не изменяя при этом величину .
Проекция вектора на горизонтальную
плоскость за время dt повернётся на угол dj,
причём:
2) dL = L×sina×dj, учитывая (1), выражение (2) можно переписать так:
3)
L×sina×dj = M×dt, где a - угол, который вектор составляет с вертикалью.
Если учесть, что
угловую скорость вращения вектора вокруг
оси аа находится по формуле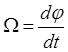 
, то из (3) можно
выразить W:
4)
.
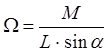В векторной форме выражение (4) записывается следующим образом:
5)
.
Таким образом, на
основании (5) можно утверждать, что под действием момента внешних сил ось гироскопа вращается
вокруг вертикальной оси с угловой скоростью W, описывая в пространстве конус. Так как, вектор не меняет своего
положения относительно вектора с
течением времени, то вращение оси гироскопа при постоянной силе является равномерным.
Такое вращение называется регулярной прецессией гироскопа, а W - угловой скоростью прецессии.
Если ось гироскопа расположена горизонтально (рис. 2), то уравнение (2) примет вид:
6)
.
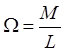Следует иметь в виду, что все приведённые рассуждения справедливы лишь для быстро вращающегося гироскопа, т.е. при
7) w0 >> W.
Тогда можно считать, что L » J0×w0, где J0 – момент инерции гироскопа относительно его собственной оси вращения; w0 – угловая скорость данного вращения. Тогда выражение (4) примет вид:
8)
.
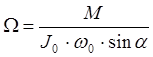При a = p/2, получаем
9)
.
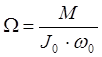При изучении прецессии гироскопов подобных конструкций следует учитывать силы возникающие в гироскопических подшипниках. Несмотря на то, что данные силы весьма молы, они приводят к усложнению прецессии. Именно из-за их действия ось ротора гироскопа при его вращении медленно наклоняется.
В данной работе требуется определить частоту оборотов ротора гироскопа по его регулярной прецессии и рассчитать момент сил трения в его подшипниках.
Из (9) следует, что:
10)
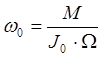, где M – момент внешних сил, задаваемый неким грузом P; M
= pl = mgl; J0 - момент инерции ротора; W - угловая скорость прецессии; l – плечо момента силы M; p – сила тяжести груза P, создающего момент M.
При M =const, угловая скорость прецессии W тоже будет постоянной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
