Устройство цифровой оптимальной обработки радиолокационного сигнала. РЛС со сжатием импульсов. Фазоманипулированные сигналы, страница 4

Для непериодического сигнала средний уровень боковых лепестков на временной оси равен –1/2. Структура боковых лепестков каждой половины автокорреляционной функции обладает относительно этого значения нечетной симметрией. Периодическую АКФ можно рассматривать как результат наложения последовательных непериодических АКФ, каждая из которых смещена по временной оси на Nt₀. В следствие нечетной симметрии непериодической структура боковых лепестков периодической функции принимает вид постоянного уровня высотой равной –1. При выделении из периодической последовательности одной полной последовательности это свойство постоянного уровня боковых лепестков пропадает.

3.5 Согласованная фильтрация сложных сигналов

Согласованные линейные фильтры (СФ) предназначены для выделения сигнала на фоне шумовой помехи, спектр которой перекрывает спектр сигнала. В них используется частотная и относительные амплитудная и фазовая селекция (СФ "реагирует" не на абсолютные значения амплитуд и фаз гармонических составляющих сигнала, а на их относительные значения). СФ дают максимально возможное отношение пикового значения сигнала к среднеквадратическому значению шума при отмеченных видах селекции. Слово "согласованный" отражает то обстоятельство, что коэффициент передачи фильтра согласован со спектральной характеристикой сигнала.

Согласованные фильтры широко применяются в радиолокации. Они являются неотъемлемой и важнейшей частью оптимальных устройств обнаружения и измерения параметров сигнала. Поскольку в этом случае они выполняют одну из основных операций обработки сигналов, иногда их называют оптимальными. Кроме обеспечения максимального отношения сигнал/шум, важным свойством СФ является сжатие сложного сигнала по времени (обострение пика сигнала) или сжатие спектра сложного сигнала, благодаря чему СФ могут выполнять роль главных элементов схем селекции по дальности и скорости, а также дискриминаторов, с помощью которых определяются величины смещения сигналов по времени запаздывания (дальности) и доплеровской частоты (скорости).

3.5.1 Эффект временного сжатия сложных сигналов в СФ

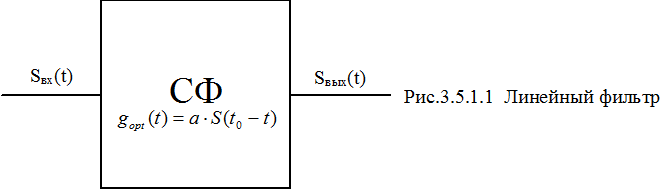
При воздействии на линейный фильтр (рис.3.5.1.1) аддитивной смеси известного сигнала и белого шума  можно получить на выходе наибольшее возможное отношение пикового значения сигнала к среднеквадратическому значению шума, если комплексный коэффициент передачи такого фильтра определяется выражением:

                                     (3.6)

или                                                                      (3.7)

Здесь            - комплексно-сопряженный спектр входного сигнала,

                  a - коэффициент пропорциональности,

                  t₀ - время, при котором отношение сигнал/шум становится максимально возможным.

Для физической реализуемых фильтров время задержки t₀³T.

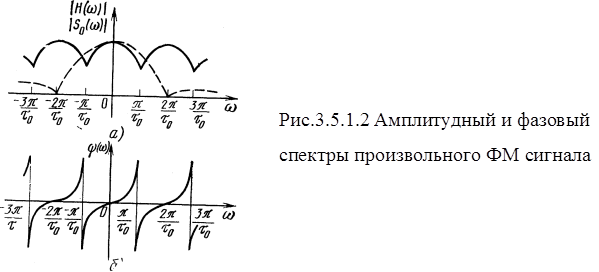
Импульсная характеристика СФ определяется как функция

                                            (3.8)

т. е. импульсная характеристика по своей форме должна совпадать с зеркальным отображением сигнала [5].

Сигнал на выходе согласованного фильтра равен , т. е. сигнал с точностью до постоянного коэффициента a совпадает с АКФ входного сигнала S(t). В момент времени t=t₀ выходной сигнал имеет пиковое значение , где E_s – энергия сигнала S(t).

Энергия сигнала S(t) определяется выражением (равенство Парсеваля) [14]

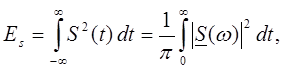                                   (3.9)

где            - есть энергетический спектр сигнала S(t), показывающий распределение энергии сигнала по частоте.

          Корреляционная функция шума на выходе согласованного фильтра K_вых(t) по форме совпадает с АКФ сигнала R(t):

               (3.10)

Здесь G₀ - энергетический спектр белого шума (G₀=const).

          Дисперсия (средняя мощность) шума на выходе может быть найдена в виде[15].

          Максимально возможное отношение сигнал/шум (по напряжению) на выходе фильтра

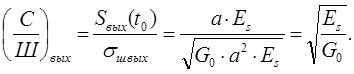                          (3.11)

Выигрыш по напряжению в отношении сигнал/шум, реализуемый при оптимальной фильтрации, находиться как

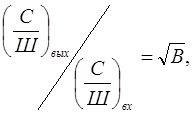                                       (3.12)

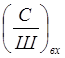где           - отношение сигнал/шум на входе фильтра,

        B - база сигнала, определяемая шириной его спектра Df и длительностью T:

                                              (3.13)

Из выражения (3.12) видно, что оптимальная фильтрация  сложных сигналов с большой базой (B>>1), которыми являются ФМ сигналы, приводит к существенному выигрышу в отношении сигнал/шум. При этом база ФМ сигнала B будет зависеть от числа m импульсов (дискретов).

Корреляционная функция сигнала обычно имеет протяженность порядка 1/Df. Таким образом, исходный сигнал длительностью T в оптимальном фильтре преобразуется в сигнал длительностью 1/Df =T/B; при B>>1 выходной сигнал  значительно короче входного, т. е. в согласованном фильтре происходит сжатие сигнала.