Устройство цифровой оптимальной обработки радиолокационного сигнала. РЛС со сжатием импульсов. Фазоманипулированные сигналы, страница 3

Оптимальная обработка принятых сигналов производится либо с помощью согласованных фильтров, либо с помощью корреляторов.

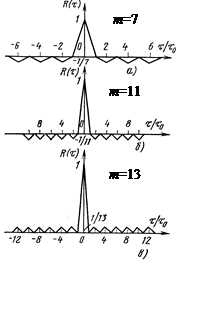
Рис.3.3.1. АКФ сигналов

Баркера с m=7, 11, 13

Коды Баркера были бы идеальными кодами при использовании их в РЛС со сжатием импульсов, если бы можно было получить такие коды большей длинны. В РЛС со сжатием импульсов, в которой используются упомянутые коды, максимально достижимый коэффициент сжатия не превышает 13.

Попытки найти коды Баркера и для m>13 не увенчались успехом. Исследования многих авторов (Ивановой, Турина, Сторера и др.) показали, что кодов с остатками величины 1/m для m>13 не существует, но для больших m возникла потребность составить коды, имеющие остатки несколько большие, чем 1/m. Одним из классов таких кодов являются М-последовательности или нуль-последовательности максимального периода.

3.4 М-последовательность

          Коды таких ФМ сигналов описываются линейными рекуррентными последовательностями [13]. Алгоритм построения М-последовательностей сводиться к следующему. Задается произвольно набор чисел y₁, y₂, …, y_n, каждое из которых равно либо нулю, либо единице, и начальная последовательность чисел q₁, q₂, …, q_n-1, каждое из которых равно либо +1, либо –1. Можно образовать следующий член последовательности q_n с помощью произведения:

                                           (3.3)

Очевидно, q_n равно либо +1, либо –1. Дальнейшие члены определяются рекуррентным соотношением

                                           (3.4)

          Так образуется бесконечная последовательность чисел {q}.

Таким образом, чтобы построить линейную рекуррентную последовательность, задаются произвольной линейной комбинацией n чисел и далее, следуя определенным рекуррентным правилам, определяют всю последовательность. После некоторого числа членов эта последовательность начинается повторяться, причем максимальный период повторения составляет:

                                                  (3.5)

Среди всех последовательностей в радиолокации предпочтение отдают двоичным М-последовательностям.

Важными для радиолокации свойствами М-последовательностей являются следующие:

·  М-последовательности являются периодическими с периодом состоящим из m цифр (символов). У двоичной последовательности при n=2, 3, 4, 5, 6, 7, 8, 9, 10 и т. д. максимальное число неповторяющихся цифр последовательности соответственно равно m=3, 7, 15, 31, 63, 127, 255, 511, 1023 и т. д. Длина периодически повторяющейся последовательности может быть сколь угодно большой;

·  М-последовательность в общем случае состоит из нескольких видов импульсов (например, импульсы могут отличаться начальными фазами, несущими частотами и т. д.). Импульсы различного вида встречаются в периоде примерно одинаковое число раз, т. е. все импульсы распределяются в периоде равновероятно. Вследствие этого М-последовательности называют часто "псевдослучайными";

·  М-последовательности обладают свойствами "хаотичности", которое проявляется в следующем. Если из одного периода М-последовательности выбрать любые отрезки по k членов в каждом, то все они будут несовпадающими. Если последовательность образуется из цифр 0 и 1, то в упомянутых отрезках найдутся все комбинации из цифр 0 и 1;

·  автокорреляционная функция ФМ сигнала, модулированного одним периодом М-последовательности, имеет боковые лепестки порядка 1/;

·  формирование и обработку ФМ сигналов, модулированных М-последовательностями, можно производить с помощью относительно простых устройств, использующих линейные переключающие схемы на основе регистров сдвига.

У ФМ сигнала, модулированного периодически повторяющейся М-последовательностью, все боковые лепестки, заключенные между периодически повторяющимися максимумами автокорреляционной функции, равны 1/m. На рис.3.4.1. приведены автокорреляционные функции периодических и непериодических сигналов для типичной последовательности максимальной длительности из 15 элементов, полученной с помощью генератора на регистре сдвига.

Рис.3.4.1. АКФ для периодических (а) и непериодических (б) последовательностей

Для периодического сигнала уровень боковых лепестков постоянен и равен –1. АКФ имеет периодический характер с периодом Nt₀, пиковое значение равно m, где m - число подымпульсов в последовательности.