ФМ
сигналы дискретные, поэтому ограничиваются возможности формирования желаемой
формы функции неопределенности.
Если
используется последовательность, состоящая из m импульсов (дискретов), и
в которой кодирование происходит с помощью двух значений фазы, то можно
составить M=2m различных
сигналов. Число дискретов m равно m=T/t0, где Т - длительность сигнала. На практике используются сигналы
с числом дискретов от десятков до тысяч. Поэтому число различных ФМ сигналов
очень велико. Чтобы построить хороший сигнал, необходимо из 2m кодовых комбинаций выбрать те, которые дают наилучшее приближение
нормированной двумерной функции автокорреляции (НДАФ) к желаемой форме.
Значительный
интерес, проявляемый в радиолокации к ФМ сигналам, связан, во-первых, с
относительно равномерным распределением боковых лепестков НДАФ при большом
числе дискретов на всей плоскости t
и FД. Во-вторых, у таких сигналов амплитуда постоянна.
Приняв
во внимание, что функция корреляции прямоугольного импульса (дискрета) имеет
треугольную форму и произведя некоторые расчеты [2],
функция корреляции ФМ сигнала представляет собой ломаную линию (рис.3.2.1.в),
способную изменять наклон лишь в точках t=lt0, где l=0,1,2,…m.

На рис.3.2.1.а изображена комплексная
огибающая (в данном случае действительная функция времени) ФМ сигнала с единичным
прямоугольным импульсом для m=5,
на рис.4.2.1.б - решетчатая функция ФМ сигнала, на
рис. 3.2.1.в - решетчатая АКФ. Тонкими линиями на рис.3.2.1.в показана АКФ ФМ
сигнала.
Интерес
представляют максимумы функции корреляции, поэтому рассматриваются значения
функции в моменты времени lt0. Если выделить огибающую сигнала с
бинарной фазовой манипуляцией и принять при анализе амплитуду равную единице,
то функция корреляции огибающей сигнала будет определяться законом изменения
фазы этого сигнала, т. е. фактически последовательностью двоичных чисел.
Следовательно
синтез ФМ сигнала по заданной функции корреляции при бинарной фазовой
манипуляции по существу сводиться к выбору последовательности двоичных чисел.
Предельные
значения нормированной функции автокорреляции ФМ сигнала равны:
(3.1)
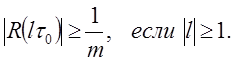 Абсолютная величина максимумов боковых лепестков функции
корреляции удовлетворяет условию:
Абсолютная величина максимумов боковых лепестков функции
корреляции удовлетворяет условию:
(3.2)
Как
видно, у ФМ сигналов минимально достижимый уровень боковых лепестков обратно
пропорционален числу дискретов (для М-последовательности обратно пропорционален
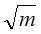 ). Этим и
объясняется стремление использовать ФМ сигналы с большим числом дискретов.
). Этим и
объясняется стремление использовать ФМ сигналы с большим числом дискретов.
При
синтезе ФМ сигналов по произвольным НДАФ основное внимание уделялось не сколько
разработке методов синтеза, сколько отысканию конкретных сигналов, обладающих,
если не оптимальными, то по крайней мере удовлетворительными свойствами и в
первую очередь малыми остатками. Путем подбора были найдены последовательности
(коды) для m=2,
3, 4, 5, 7, 11, 13, которые называются кодами Баркера.
3.3 Коды Баркера
Сигналы, соответствующие
кодам Баркера, являются уникальными ФМ сигналами. В таблице 3.1. приведены
значения кодов Баркера и значения функций корреляции "определяющих точек".
Таблица 3.1.
|
Число
дискре-тов
|
Последовательность
Баркера
|
АКФ
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
|
2
2
4
4
5
7
11
13
|
1 -1
1 1 -1
1 1 -1 1
1 1 1 -1
1 1 1 -1 1
1 1 1 -1 -1 1
–1
1 1 1 -1 -1 -1
1 -1 -1 1 -1
1 1 1 1 1 -1 -1
1 1 -1 1 -1 1
|
2 -1
3 0 -1
1 -1 0
-1
4 1
0 -1
5 0
1 0 1
7 0
-1 0 -1 0 -1
11 0 -1
0 -1 0 -1 0 -1 0 -1
13 0
1 0 1 0 1 0 1 0 1 0 1
|
На рис.3.3.1. показаны
автокорреляционные функции кодов Баркера для m=7, 11, 13.
Кроме приведенных кодов, коды Баркера
получаются, если знаки, приведенные в таблице 3.1., изменить на обратные или
использовать так называемые инверсные коды, имеющие обратный порядок знаков
(справа налево), но и они обладают такими же автокорреляционными функциями.
Формирование сигналов, модулированных
кодами Баркера, чрезвычайно простое. Это является еще одним из преимуществ,
почему их широко используют в радиолокации.

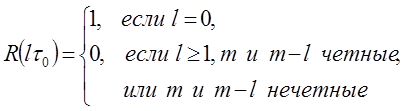
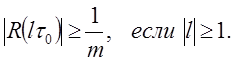 Абсолютная величина максимумов боковых лепестков функции
корреляции удовлетворяет условию:
Абсолютная величина максимумов боковых лепестков функции
корреляции удовлетворяет условию: